A Circle and a Centroid
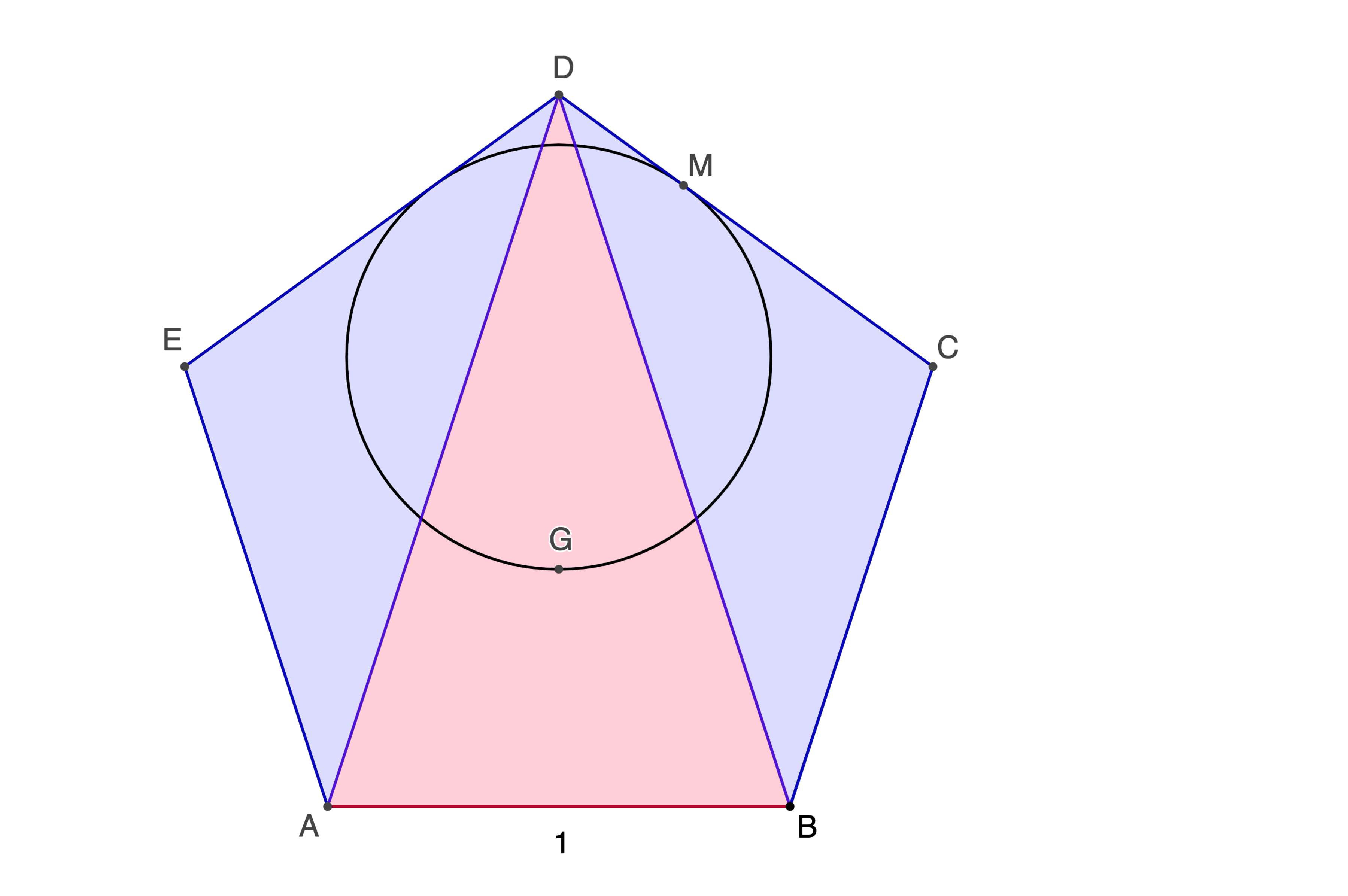
A B C D E is a regular unit pentagon. G is the centroid of △ A B D . A circle is drawn through G such that it is tangent with the pentagon at M . If the length of D M is q p , where p and q are positive co-prime integers, submit p + q .
Bonus: find the radius of the circle.
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Thank you, Thanos. It's always a joy to read your solutions. I hadn't thought of the homothecy angle. Nice insight.
Log in to reply
Hi Fletcher! I 'm glad you liked the solution. It is funny, I thought the homothecy was your initial approach, since you asked for the radius secondarily. Is there a more straightforward way to solve the problem?
Log in to reply
In my first design of the problem, I was going to ask for the radius. I hadn't even noticed that D M = 3 1 ! When I discovered that nice number, I switched my question, since I always ask for complicated expressions and I felt folks are probably getting annoyed about that. :)
Point G as a centroid is always at a height 1/3 of the apex from the base, and since ABD is an isosceles triangle, DG is perpendicular to AB, with twice the length of G to AB distance. If we draw a smaller regular pentagon with D being one of the vertices and the circle as its incircle, it's easy to see that one of its other vertices would be the midpoint of MC. It's equivalent to enlarging the circle to be ABCDE's incircle so that G' touches the AB base and M' becomes the midpoint of DC.
DM / DM' = DG / DG'
DM / (1/2) = (2h/3) / (h)
DM = (1/2) × (2/3) = 1/3
Answer = 1 + 3 = 4
Bonus : the r would also be 2/3 of a regular unit pentagon's incircle, so
r = (2/3) × ( √(25 + 10√5) / 10 )
= √(25 + 10√5) / 15
You always make it seem so easy, Saya.
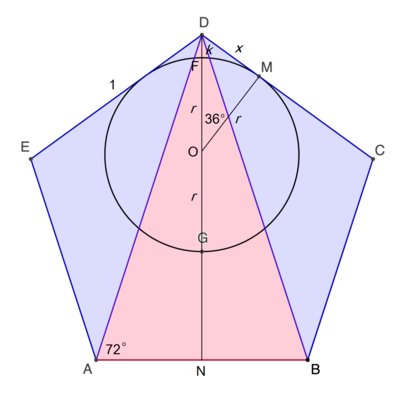
Let D N be perpendicular to A B ; and the circle has a center at O and intersects D N at F and G . We note that ∠ D A B = 7 2 ∘ and ∠ D O M = 3 6 ∘ . The the altitude D N = 2 1 tan 7 2 ∘ . Since G is the centroid of △ A B D , D G = 3 2 ⋅ D N = 3 tan 7 2 ∘ .
Let the radius of the circle be r , D F = k , and D M = x . Then D G = k + 2 r ⟹ k = 3 tan 7 2 ∘ − 2 r and x = r tan 3 6 ∘ . By tangent-secant theorem ,
x 2 r 2 tan 2 3 6 ∘ r 2 tan 2 3 6 ∘ r 2 ( 1 + tan 2 3 6 ∘ ) r 2 sec 2 3 6 ∘ ⟹ r x = k ( k + 2 r ) = ( 3 tan 7 2 ∘ − 2 r ) 3 tan 7 2 ∘ = ( 3 tan 7 2 ∘ − r ) 2 − r 2 = ( 3 tan 7 2 ∘ − r ) 2 = ( 3 tan 7 2 ∘ − r ) 2 = 3 ( 1 + sec 3 6 ∘ ) tan 7 2 ∘ = r tan 3 6 ∘ = 3 ( 1 + sec 3 6 ∘ ) tan 7 2 ∘ tan 3 6 ∘ = 3 cos 7 2 ∘ ( cos 3 6 ∘ + 1 ) 2 sin 2 3 6 ∘ cos 3 6 ∘ = 3 ( 2 cos 2 3 6 ∘ − 1 ) 2 ( 1 − cos 3 6 ∘ ) cos 3 6 ∘ = 3 ( φ 2 − 2 ) 2 φ − φ 2 = 3 ( φ + 1 − 2 ) 2 φ − φ − 1 = 3 1 Note that cos 3 6 ∘ = 2 φ , where φ = 2 1 + 5 is the golden ratio.
Therefore p + q = 1 + 3 = 4 .
Simple angle chasing gives that ∠ D O M = ∠ D G K = 3 6 ∘ .
For the angles 3 6 ∘ and 7 2 ∘ we use the following trigonometric values: cos 3 6 ∘ = 2 φ tan 3 6 ∘ = φ 3 − φ tan 7 2 ∘ = φ − 1 2 + φ where φ is the golden ratio 2 1 + 5 .
First,
D G = 3 2 D F = 3 2 ⋅ F B ⋅ tan 7 2 ∘ = 3 2 ⋅ 2 1 ⋅ φ − 1 2 + φ = 3 1 ⋅ φ − 1 2 + φ Hence,
G K = D G ⋅ cos 3 6 ∘ = 3 1 ⋅ φ − 1 2 + φ ⋅ 2 φ ( 1 ) On the other hand,
G K = G L + L K = R ⋅ cos 3 6 ∘ + R = R ⋅ ( 2 φ + 1 ) ( 2 ) Combining ( 1 ) and ( 2 ) ,
R ⋅ ( 2 φ + 1 ) = 3 1 ⋅ φ − 1 2 + φ ⋅ 2 φ ⇒ R ⇒ R = 3 1 ⋅ 3 − φ 2 + φ since φ 1 = φ − 1 = 3 1 ⋅ ( φ − 1 ) ( φ + 2 ) φ 2 + φ = 3 1 ⋅ φ 2 + φ − 2 φ 2 + φ = 3 1 ⋅ 2 φ − 1 φ 2 + φ since φ 2 = φ + 1 = 3 1 ⋅ 2 − φ 1 2 + φ
Finally, D M = O M ⋅ tan 3 6 ∘ = R ⋅ tan 3 6 ∘ = 3 1 ⋅ 3 − φ 2 + φ ⋅ φ 3 − φ = 3 1 ⋅ 3 φ − φ 2 6 + φ − φ 2 = 3 1 ⋅ 2 φ − 1 5 since φ 2 = φ + 1 = 3 1
For the answer, p = 1 , q = 3 , thus, p + q = 4 .
2nd proof (using homothecy)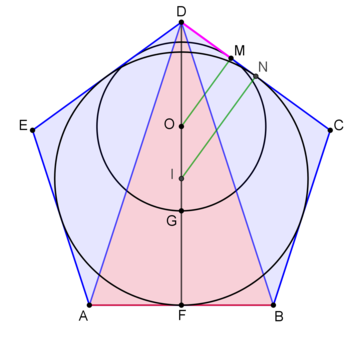 The circle we are interested in is the image of the incircle of the regular pentagon, with homothetic center point
D
and scale factor
r
=
D
F
D
G
=
3
2
.
The circle we are interested in is the image of the incircle of the regular pentagon, with homothetic center point
D
and scale factor
r
=
D
F
D
G
=
3
2
.
Since the point of tangency of the incircle with side D C is the midpoint N of D C and its image is M it holds that
D N D M = r ⇒ D M = r ⋅ D N = 3 2 ⋅ 2 1 D C = 3 1 Likewise, the radius R of the circle is 3 2 that of the radius of the incircle, thus,
R = 3 2 ⋅ 1 0 1 2 5 + 1 0 5 = 1 5 2 5 + 1 0 5