A circle and a pentagon

Geometry Level 3

Pictured here is a ${\color{#3D99F6} \text{regular pentagon}}$ which has one vertex on a ${\color{#69047E} \text{unit circle}}$ , and the ${\color{#20A900} \text{green line segments}}$ connect vertices of the pentagon:

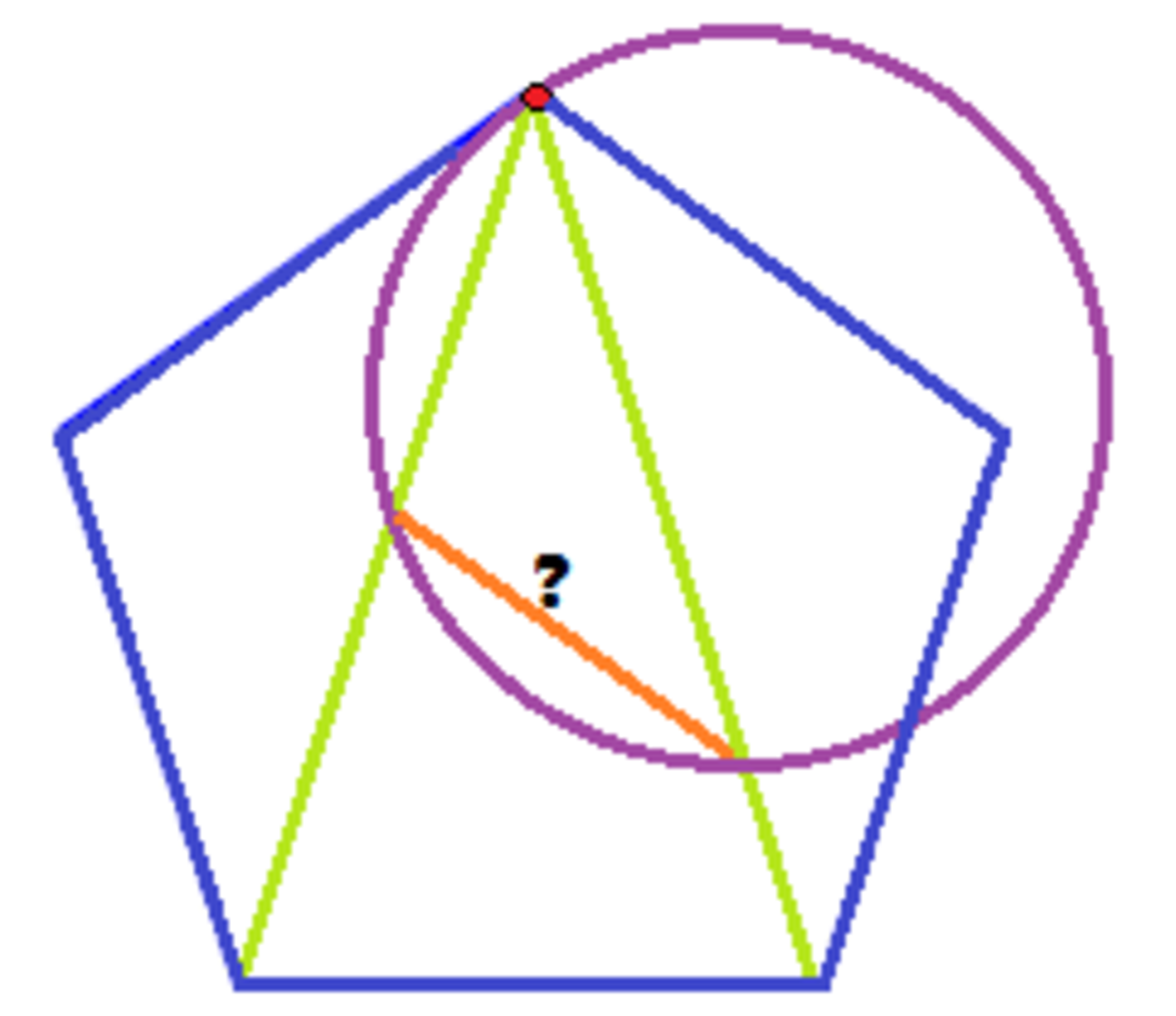
What is the length of the ${\color{#EC7300} \text{orange line segment}}$ ?

Provide your answer to 3 decimal places. If you think not enough information is given, submit -1 as your answer.

Note : The circle isn't necessarily tangent to any of the line segments drawn.

The answer is 1.176.

1 solution

Geoff Pilling
Jul 1, 2017

The green segments make up two of the lines of a pentagram (5 pointed star) inscribed inside the pentagon. So, they have an angle of $36^\circ$ with respect to each other:

Therefore the angle of the black lines connecting at the center of the circle will be $72^\circ$ .

And, so, from the law of cosines applied to the triangle made up of the two black lines and the orange line, if $x$ is the length of the orange line, then:

$x^2 = 1^2 + 1^2 - 2\cdot 1 \cdot 1 \cdot \cos(72^\circ)$

$\implies x = \boxed{1.176}$

U can also use sine rule here because the triangle with two green segment and one orange segment is inscribed in the unit circle so, $\dfrac{x}{\sin 36}=2R=2 \times 1 \\ x=2 \sin 36$

The best thing of the problem is that the length of orange segment doesn't depend upon the side-length of pentagon

Kushal Bose - 3 years, 11 months ago

A circle and a pentagon

The answer is 1.176.

1 solution

0 pending reports