A Circle and a Square sharing an Area
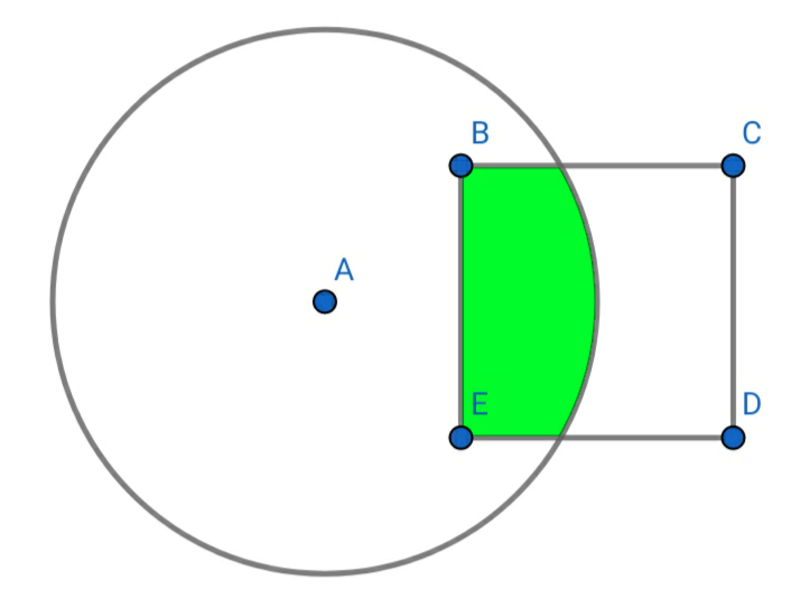
Circle A has a radius of 1 and square B C D E of side length 1 has center on the circle's circumference. The square is positioned in such a way that its top and bottom sides are parallel to the circle's horizontal diameter.
Find the area of the shaded region.
The answer is 0.4566.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
To get the area of the shaded part, we need to get the area of the rectangle B F G E and the segment of ∠ G A F and add them.
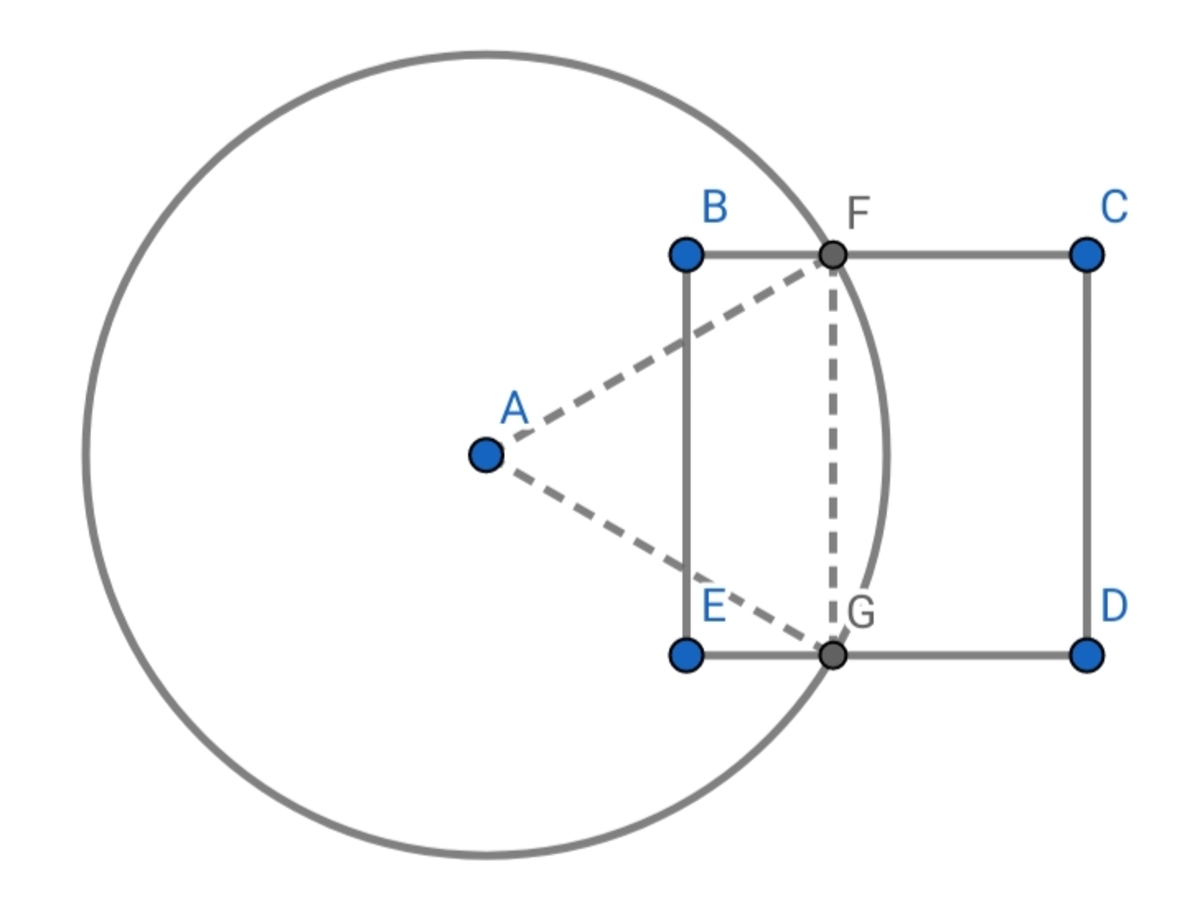
Line segment F G has the same length as the side of the square which is 1 . Since A G and A F are radii, they form an equilateral triangle together with F G which means ∠ G A F must be 6 0 ° . We can now then compute for the area of the segment.
1 2 ( 3 6 0 6 0 π − 2 sin ( 6 0 ° ) ) ≈ 0 . 0 9 0 5 8 6
In order to find the area of rectangle B F G E , we must first find the length of B F .
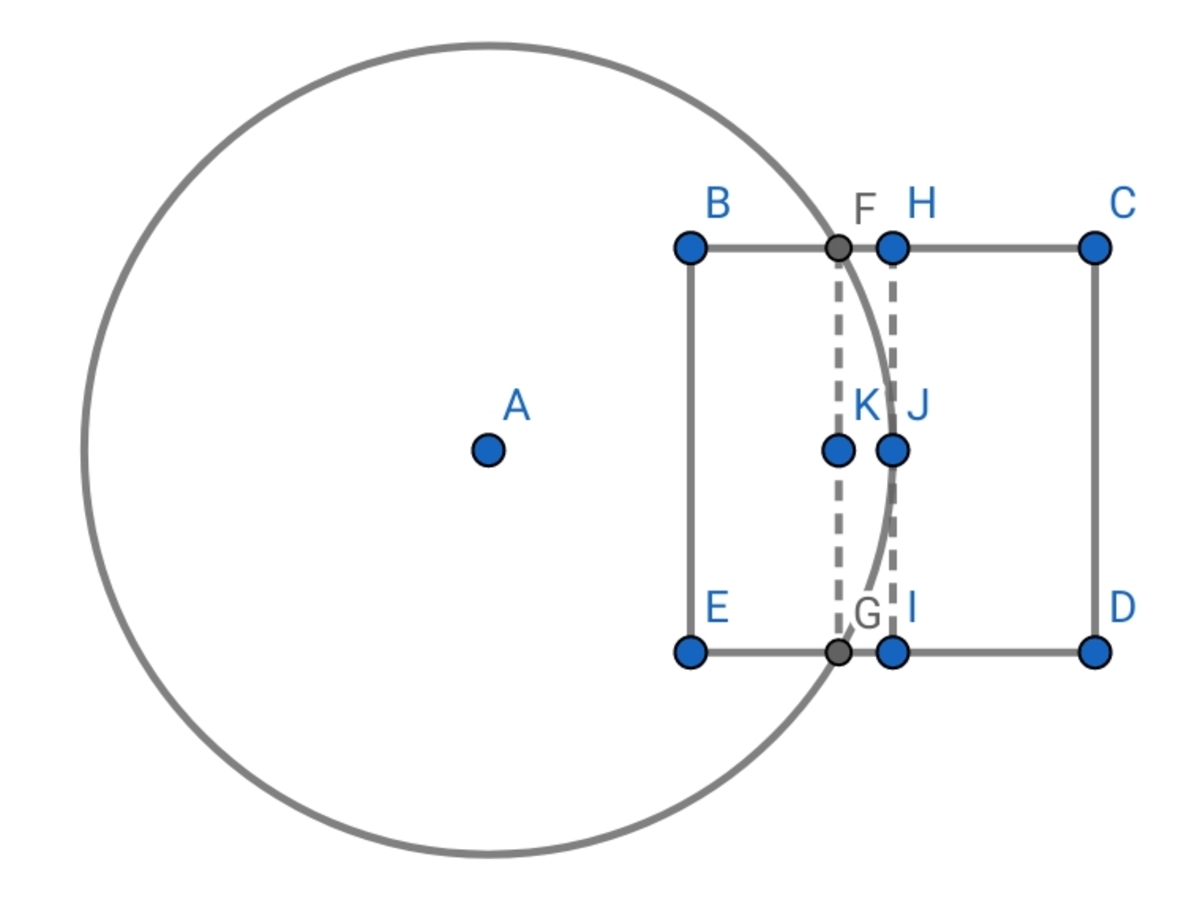
The length between K and J is the same as the length of F H .
F H = K J = x
Line segment L J is the circle's diameter. Thus, K J = x and L K = 2 − x . We can use the Intersecting Chords Theorem to get the value of x .
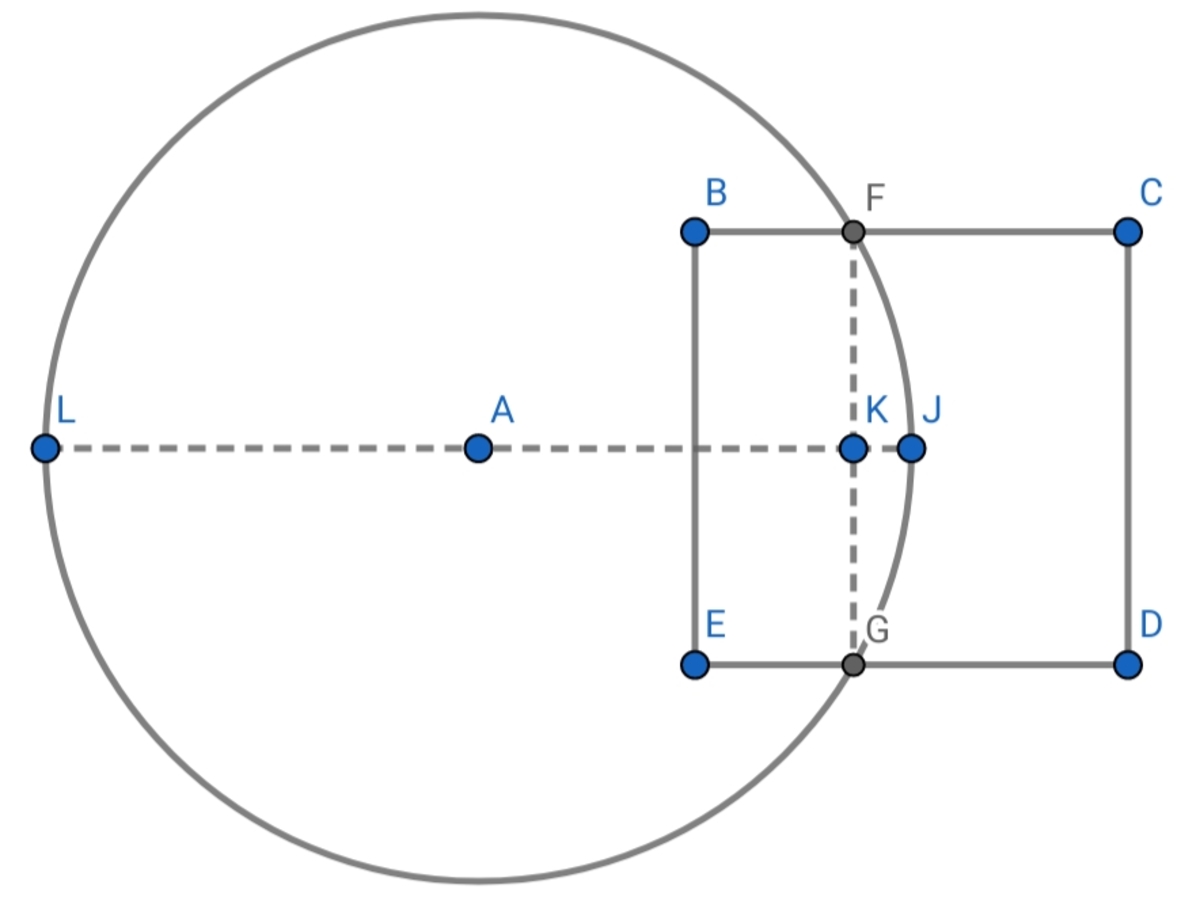
L K × K J ( 2 − x ) × x − x 2 + 2 x − x 2 + 2 x − 4 1 = F K × K G = 2 1 × 2 1 = 4 1 = 0
The roots of the quadratic equation above are 1 + 2 3 and 1 − 2 3 . Since the value we're looking for x is less than 1 , we take the latter root which is approximately 0 . 1 3 3 9 7 5 . The length of B F is 2 1 , which is the length of B H , minus x . The rectangle's area can now be calculated and it is 0 . 3 6 6 0 2 5 . We add up the segment's area and the rectangle's and we get the answer, rounded to the nearest ten-thousandths, 0 . 4 5 6 6 .
@Kaizen Cyrus , you need not specify to the nearest ten-thousands. The system is set to only three signifant figures. Higher accuracy will not matter. You can use the picture icon (third from left) to attach your image.
Log in to reply
I'm using the mobile version so I didn't notice. When I use the Desktop view, it's such an inconvenience to navigate and click. The icon doesn't seem to be working to me for now.
And it seems like the app version doesn't let you upload images to solutions.
Let the green region be defined by: 2 1 ≤ x ≤ 1 − y 2 , − 2 1 ≤ y ≤ 2 1 such that orgin of the x y − plane lies at A above. Integrating with respect to y yields:
∫ − 2 1 2 1 1 − y 2 − 2 1 d y = 2 y 1 − y 2 + 2 1 arcsin ( y ) − 2 y ∣ − 2 1 2 1 = 6 π − 2 1 + 4 3 .
The area of the shade region A is made up two parts rectangle B F G E and circular segment F G (in pale blue). To find the area of segment A segment , we minus the area of △ A F G , A △ , from the area of sector A F G , A sector . In equation, we have:
A = A B F G E + A segment = B F × B E + A sector − A △ = ( h − 2 1 ) × 1 + 3 6 0 ∘ 6 0 ∘ π − 2 1 ( 1 ) ( 1 ) sin 6 0 ∘ = 2 3 − 2 1 + 6 π − 4 3 = 4 3 − 2 1 + 6 π ≈ 0 . 4 5 7 Note that △ A F G is equilateral. ⟹ ∠ F A G = 6 0 ∘ and h = 2 3