A circle and equilateral triangle inscribed in a semicircle.
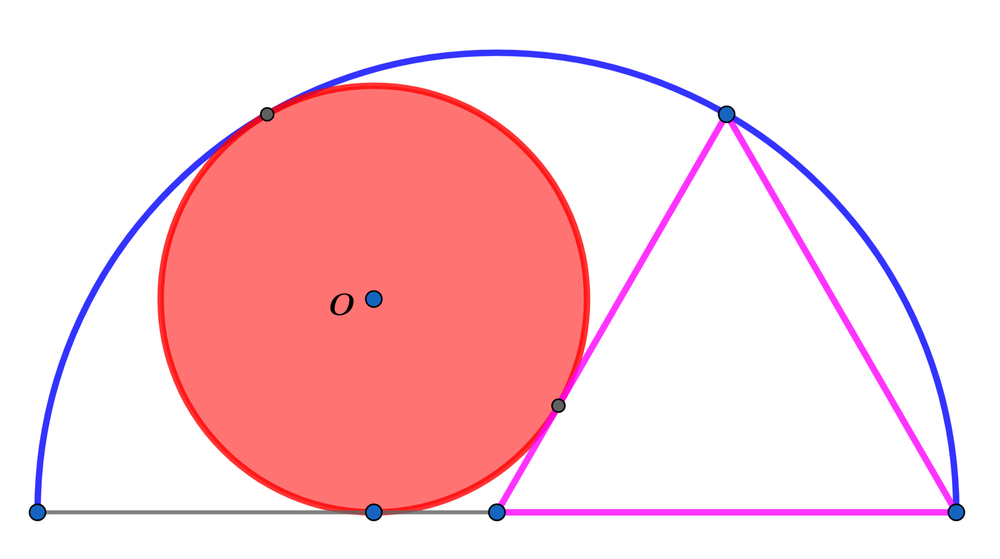
A circle and equilateral triangle are inscribed in a semicircle with radius 1 and the circle is tangent to the semicircle and equilateral triangle as shown above and one of the vertices of the equilateral triangle is at the center of the semicircle.
If the area of the circle A c = α ( β − λ α ) π , where α , β and λ are coprime positive integers, find α + β + λ .
The answer is 14.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Are there any typos in the second line? Should A B E be A B C and should N R E be N O E ?
Log in to reply
Yes there is. It should be:
m ∠ C F D = 6 0 ∘ ⟹ m ∠ A F C = 1 2 0 ∘ and letting m ∠ N O E = θ ⟹
1 2 0 ∘ = 2 1 ( m ( N B E ) − m ( N R E ) ) = 2 1 ( 3 6 0 ∘ − 2 θ ) ⟹
2 4 0 ∘ = 3 6 0 ∘ − 2 θ ⟹ θ = 6 0 ∘ ⟹ m ∠ N O F = 3 0 ∘ ⟹
∠ O F N = 6 0 ∘
and I forgot to put the R in the diagram for N R E . I'll add it. Thanks!
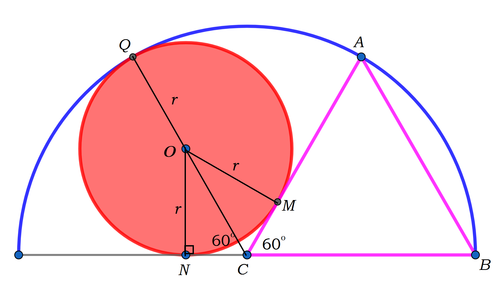
Let the equilateral triangle be A B C , where C is the center of the semicircle, the tangent points to equilateral triangle, the semicircle diameter, and the semicircle arc be M , N , and Q respectively, and the radius of the circle be r . Then O M = O N = O Q = r , where O is the center of the circle, and they are perpendicular to the respective line.
We note that C , O , and Q are colinear. Since △ A B C is equilateral, ∠ A C B = 6 0 ∘ , ⟹ ∠ A C N = 1 8 0 ∘ − 6 0 ∘ = 1 2 0 ∘ . Due to symmetry, ∠ O C M = ∠ O C N = 6 0 ∘ . Then
Q O + O C Q O + O N csc ∠ O C N r + r csc 6 0 ∘ r ⟹ A c = Q C = Q C = 1 = 1 + csc 6 0 ∘ 1 = 1 + 3 2 1 = 3 + 2 3 = 4 − 3 3 ( 2 − 3 ) = 2 3 − 3 = π r 2 = ( 2 3 − 3 ) 2 π = ( 2 1 − 1 2 3 ) π = 3 ( 7 − 4 3 ) π
Therefore α + β + γ = 3 + 7 + 4 = 1 4 .
m ∠ C F D = 6 0 ∘ ⟹ m ∠ A F C = 1 2 0 ∘ and letting m ∠ N O E = θ ⟹
1 2 0 ∘ = 2 1 ( m ( N B E ) − m ( N R E ) ) = 2 1 ( 3 6 0 ∘ − 2 θ ) ⟹
2 4 0 ∘ = 3 6 0 ∘ − 2 θ ⟹ θ = 6 0 ∘ ⟹ m ∠ N O F = 3 0 ∘ ⟹
∠ O F N = 6 0 ∘ ⟹ y r = tan ( 6 0 ∘ ) = 3 , where y = N F
⟹ y = 3 r ⟹ m = 3 2 r ⟹ B F = r + m = 3 2 + 3 r = 1 ⟹
r = 2 + 3 3 = 2 3 − 3 ⟹ A c = π ( 2 3 − 3 ) 2 = 3 ( 7 − 4 3 ) π
α ( β − λ α ) π ⟹ α + β + λ = 1 4