A circle and secants problem
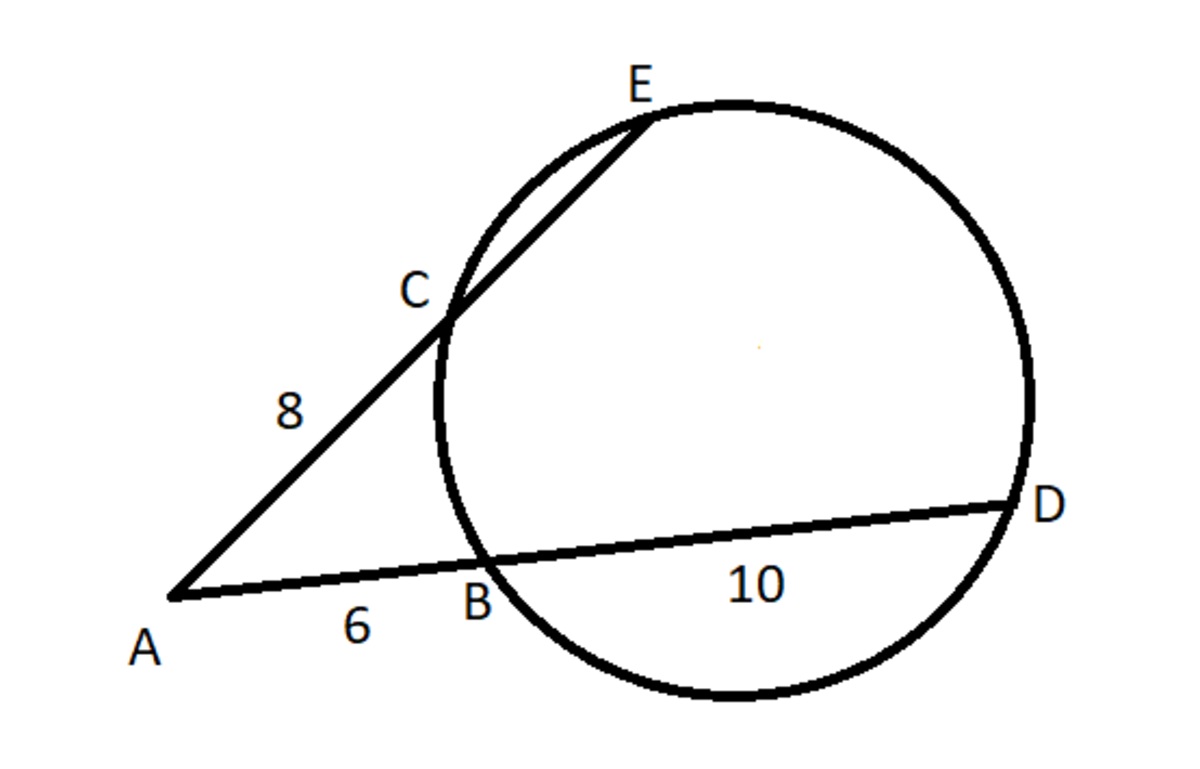
A circle is intercepted by two secants from a point A as shown in the figure. The first secant intersects the circle at points B and D , such that A B = 6 and B D = 1 0 . The second secant intersects the circle at points C and E , such that A C = 8 . If ∠ A = 6 0 ∘ , find the radius of the circle R . Submit the value of R 2 .
Figure not drawn to scale.
The answer is 52.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Having forgotten all about power of a point and intersecting secants, I did this with coordinate geometry:
Taking A as the origin, B on the axis and using the fact that ∠ A = 6 0 ∘ , we can locate points B , C , D : B ( 6 , 0 ) , C ( 4 , 4 3 ) , D ( 1 6 , 0 )
These three points lie on the circle, and are enough to define it. If the circle's centre is at ( u , v ) and its radius is R , we have ( u − 6 ) 2 + v 2 = R 2 , ( u − 4 ) 2 + ( v − 4 3 ) 2 = R 2 , ( u − 1 6 ) 2 + v 2 = R 2
The first and last of these tell us u = 1 1 (alternatively, this is just the perpendicular bisector of the chord B D ).
So 2 5 + v 2 = R 2 and 4 9 + ( v − 4 3 ) 2 = R 2
Subtracting, we find v = 3 3 , and then substituting into any of the equations gives R 2 = 5 2 .
From the intersecting secants theorem , we can determine CE
8 ( 8 + C E ) = 6 ( 1 6 )
so that C E = 4
B C can be determined from the law of cosines
B C 2 = 8 2 + 6 2 − 9 6 cos A = 6 4 + 3 6 − 4 8 = 5 2
D E can be determined from the law of cosines
D E 2 = 1 6 2 + 1 2 2 − 2 ( 1 6 ) ( 1 2 ) cos A = 2 5 6 + 1 4 4 − ( 1 9 2 ) = 2 0 8
The radius of the circle is the circumradius of cyclic quadrilateral B D E C , and this is given by Parameshvara's formula
R = 4 1 ( s − a ) ( s − b ) ( s − c ) ( s − d ) ( a b + c d ) ( a c + b d ) ( a d + b c )
where a , b , c , d are the lengths of the four sides of the cyclic quadrilateral and s is the semi-perimeter , s = 2 1 ( a + b + c + d )
So we can set
a = B C = 5 2
b = B D = 1 0
c = D E = 2 0 8
d = C E = 4
Pluggin these into the formula we get
R = 5 2
Thus the answer is R 2 = 5 2
Was it intentional that B C = 2 1 D E = R ? I wonder if this leads to another solution?
No. It wasn't intentional.
By power of a point, A B ⋅ A D = A C ⋅ A E , so A E = 8 6 ⋅ 1 6 = 1 2 .
Since ∠ E A B = 6 0 ∘ and A E = 2 A B , triangle E A B is a 3 0 ∘ − 6 0 ∘ − 9 0 ∘ triangle, so E B = 6 3 .
Since ∠ E B D = 9 0 ∘ , by Pythagoras, E D 2 = ( 6 3 ) 2 + 1 0 2 = 2 0 8 . The fact that ∠ E B D = 9 0 ∘ also implies E D is a diameter of the circle, so R 2 = 4 E D 2 = 5 2 .
Let the center of the circle be O , and let the midpoints of B D and C E be F and G , respectively. Then R = O B = O C = O D = O E .
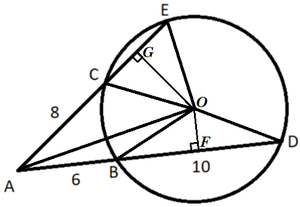
By the intersecting secant theorem , A C ⋅ A E = A B ⋅ A D , or 8 ( 8 + C E ) = 6 ⋅ 1 6 , which solves to C E = 4 .
Since F is the midpoint of B D , and B D = 1 0 , B F = 5 , and by the Pythagorean Theorem on △ B F O , O F = R 2 − 2 5 .
Similarly, since G is the midpoint of C E , and C E = 4 , C G = 2 , and by the Pythagorean Theorem on △ C G O , O G = R 2 − 4 .
From △ F A O , tan F A O = A F O F = 1 1 R 2 − 2 5 , and from △ G A O , tan G A O = A G O G = 1 0 R 2 − 4 .
By the tangent addition formula , 1 − tan F A O ⋅ tan G A O tan F A O + tan G A O = tan ( F A O + G A O ) or 1 − 1 1 R 2 − 2 5 ⋅ 1 0 R 2 − 4 1 1 R 2 − 2 5 + 1 0 R 2 − 4 = tan 6 0 ° = 3 , which solves to R 2 = 5 2 .
We note that the circle is the circumcircle of △ B C D . Then the circumradius is given by:
2 R = sin ∠ C B D C D
By cosine rule , we have:
C D 2 ⟹ C D = 8 2 + 6 2 − 2 ( 8 ) ( 1 6 ) cos 6 0 ∘ = 1 9 2 = 8 3
And
B C 2 ⟹ B C = 8 2 + 6 2 − 2 ( 8 ) ( 6 ) cos 6 0 ∘ = 5 2 = 2 1 3
By sine rule , we have:
C A sin ∠ A B C ⟹ sin ∠ A B C = B C sin ∠ C A B = 2 1 3 sin 6 0 ∘ × 8 = 1 3 1 2
Note that sin ∠ C B D = sin ( 1 8 0 ∘ − ∠ A B C ) = sin ∠ A B C = 1 3 1 2 and
2 R ⟹ R R 2 = sin ∠ C B D C D = 1 3 1 2 8 3 = 4 1 3 = 2 1 3 = 5 2