A circle and smaller square in a larger square.

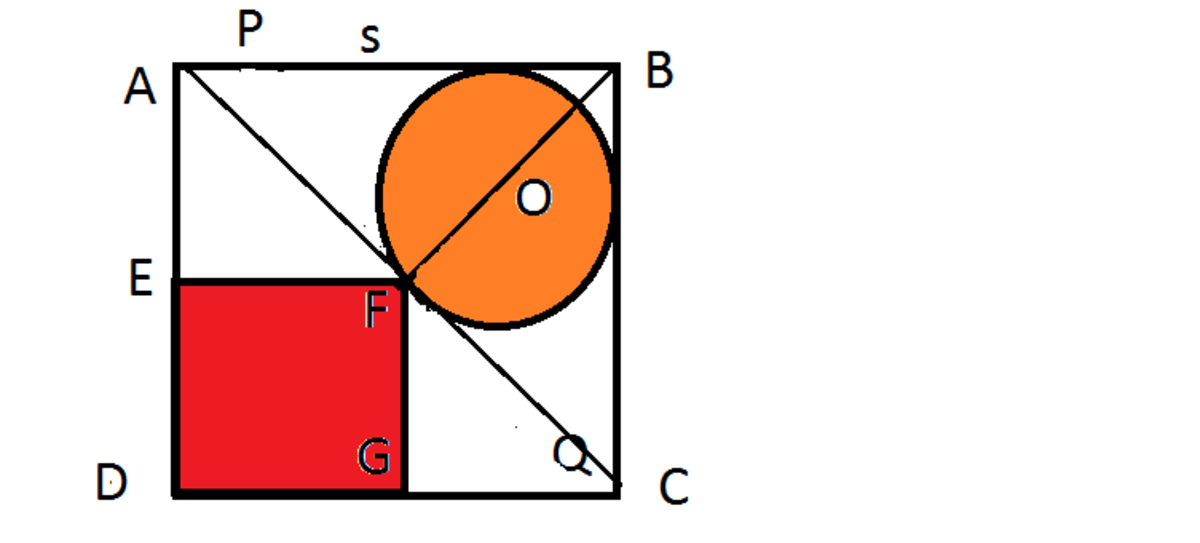
If you have a Circle and Square in a larger Square with the following dimensions:

The larger square ABCD has a side of length of s, inside this we have Smaller Square DEFG and a Circle O with a radius OF equal to half the length of the side of the smaller square (DEFG)

PQ is a tangent to the Circle O as shown in the figure which touches sides AB and BC.

Note: The length of PQ is less than the diagonal of the larger square.

let x be the length of this tangent PQ

Then x is given by the expression

x = 2s(a + b*sqrt(c))/d

Find a + b + c + d