A Circle Inside of a Square

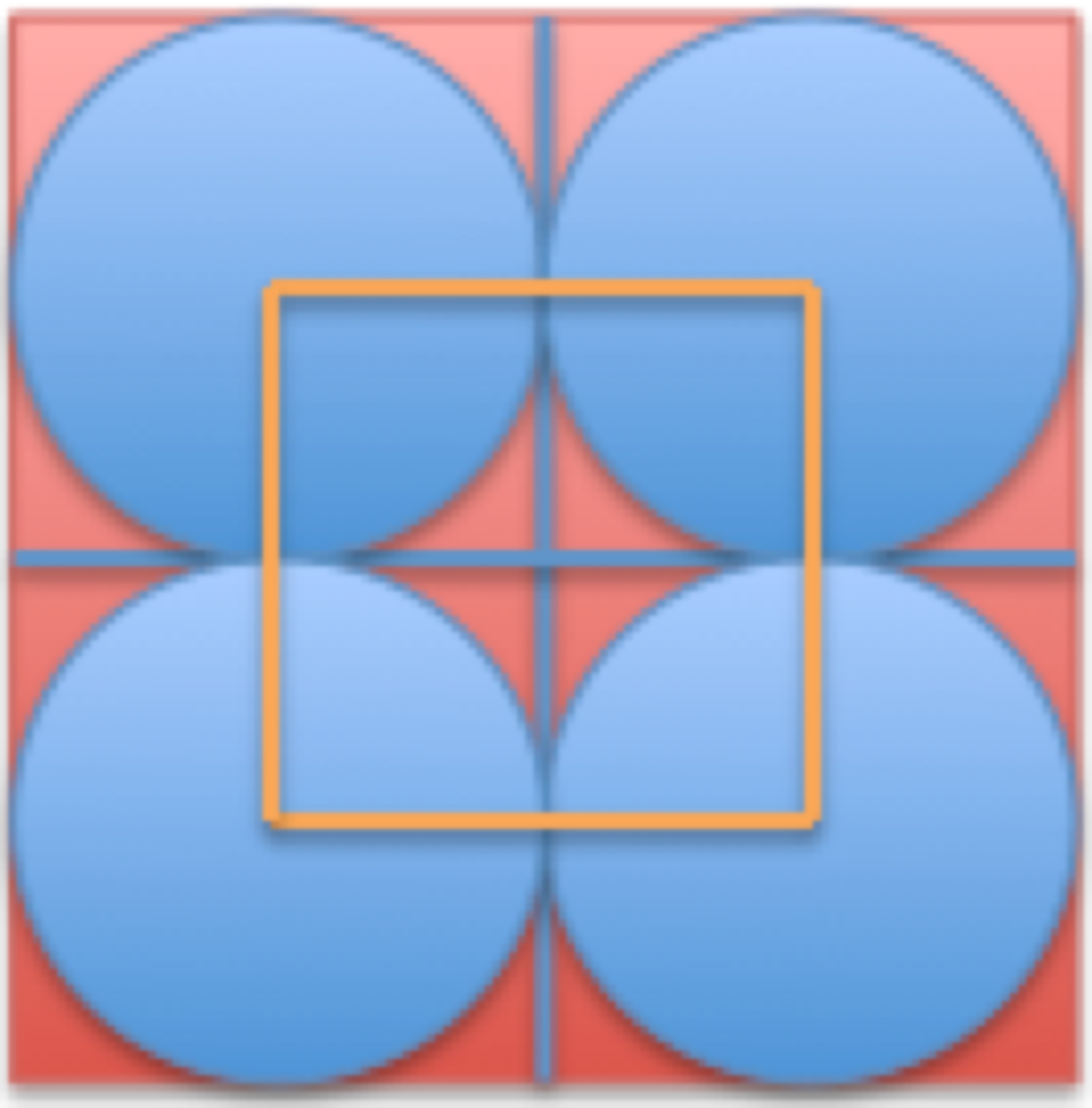Draw the circles so that they are tangent to two sides of the square as illustrated in the above photo to put the centers of the circles in the farthest spots so that all of the other possible circles can go inside of the square that is made by connecting the dots. The circle in this picture is the ring formed by the centers of the circles when the center of the square lies on the circle. So, any of the centers inside of or on this circle satisfy the conditions in the problem. The probability is the area of successful outcomes (the yellow circle) over the number of possible outcomes (the orange square). Since the side length of the orange square is twice the radius of the circle, which is $\frac{1}{2}$ the side length of the red square, the the area of all possible outcomes is $\frac{1}{4}$ the area of the red square. The radius of the yellow circle is $\frac{1}{4}$ the side length of the red square. So, the area of the yellow circle is $\frac{1}{16}$ 𝜋 the area of the red square. $\frac{1}{16}$ 𝜋 over $\frac{1}{4}$ equals $\frac{1}{4}$ 𝜋. The problem says to submit the answer as the numerator plus the denominator of the probability, so 1+4= 5 .