A Circle Inside
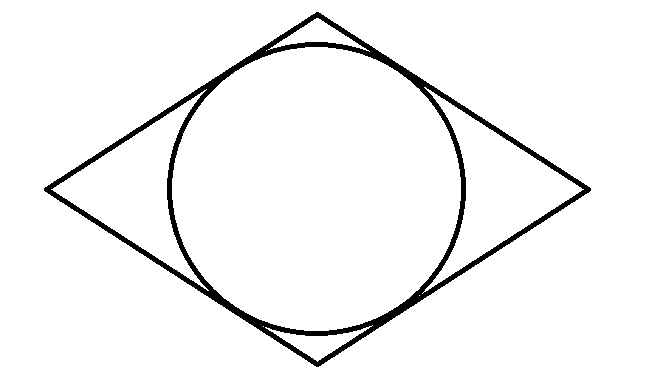
A quadrilateral above has the same length of sides, has the same opposing angles and inscribes a circle whose circumference is 8 π . Determine the area of the quadrilateral whose smaller angles are equal to 6 0 ∘ .
Give your answer to 1 decimal place.
The answer is 73.9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Same solution. :)
Very simple problem. Solved using basic trigonometry and applying the principles of simmetry. The answer is the square root of (5461 + 1/3). Generalised:
A = 2 r 2 / t a n ( 9 0 ° − α ) + 2 r 2 / t a n ( α )
Where
r = d / 2 π
This can, probably, be further simplified
But if you can't write this number in the field
Log in to reply
The question should specify what to write... I'm not the creator of the problem though. I personally put 73.9 and that made it for me
Log in to reply
We use the exact same figure in the 1st post , and the circle is labelled tangent at $Q$
So , $R=\frac{8\pi}{2\pi}=4$
Hence , we intersect the diagonals to get $AP$ as $2R$, then $\triangleQPA$ 's other leg is
$\sqrt{8^2-4^2}=4\sqrt{3}$
Also , for \$triangleQPB$ 's other leg is unknown , we label it as x .
$\therefore \tan ^30\circ=\frac{x}{4}=\frac{1}{\sqrt{3}}$
$\therefore x\sqrt{3}=4$ , after cross-multiplying .
So , $x=\frac{4}{\sqrt{3}}$
Then , $AB=4\sqrt{3}+\frac{4}{\sqrt{3}}=\frac{4\sqrt{3}*\sqrt{3}}{\sqrt{3}}+\frac{4}{\sqrt{3}}=$
$\frac{16}{sqrt{3}}$ Then , the area of the quadrilateral is $8*\frac{16}{\sqrt{3}}$ , when rounded off is $73.9$ cm$^2$, as $8$ cm is the height of the rhombus
T
a
n
(
9
0
−
α
)
=
C
o
T
a
n
(
α
)
=
T
a
n
(
α
)
1
Y
o
u
r
e
x
p
r
e
s
s
i
o
n
i
s
A
=
2
r
2
(
T
a
n
(
α
)
+
T
a
n
(
α
)
1
)
=
2
r
2
∗
T
a
n
(
α
)
S
e
c
2
(
α
)
=
S
i
n
α
4
r
2
Thanks for a nice formula. Proof can be had from the sketch I have given in my solution.
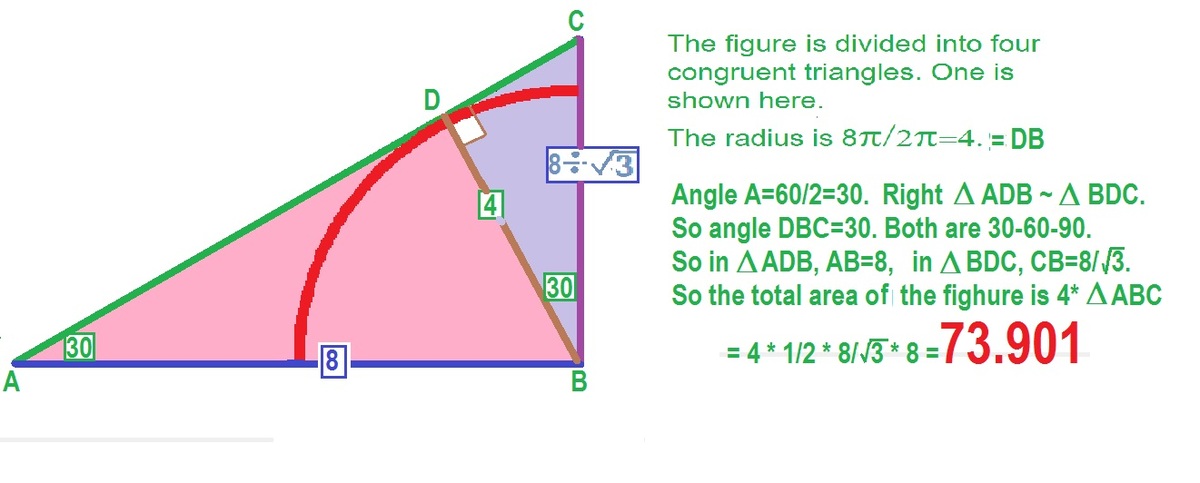
General formula for area of a rhombus when radius of the incircle r and one angle
α
is known would be,
4
∗
1
/
2
∗
A
B
∗
B
C
=
2
∗
S
i
n
(
2
1
∗
α
)
r
∗
C
o
s
(
2
1
∗
α
)
r
=
2
∗
S
i
n
(
2
1
α
)
∗
C
o
s
(
2
1
∗
α
)
r
2
,
S
i
n
c
e
2
∗
S
i
n
(
2
1
∗
α
)
∗
C
o
s
(
2
1
∗
α
)
=
S
i
n
(
α
)
,
.
.
.
.
A
r
e
a
=
S
i
n
α
.
4
r
2
I actually managed to solve this all in my head. Took me a day on and off whilst walking the dog. Got 128/3 * sqrt(3) but did need a calculator to convert that to decimal. Radius=4 and the rest was similar triangles using 1,2,sqrt(3) as the 3 sides to get the side length of the equilateral as 16/3 * sqrt(3). The vertical was 8. Easy then to get area of equilateral triangle and double for quadrilateral.
Relevant wiki: Incircles and Excircles