Biggest Cylinder To Fit In A Cone

Since we know a cylinder and a cone are solids of revolution we can assume that to get a maximum volume of our solid, we need the maximum area of the polygon that we are going to rotate, so we work with a rectangle with side lenghts r and h for our cylinder, and a triangle rectangle with height a and base b . The rectangle is obviuosly inscribed in the triangle with its side r on the base b of the triangle, something as the image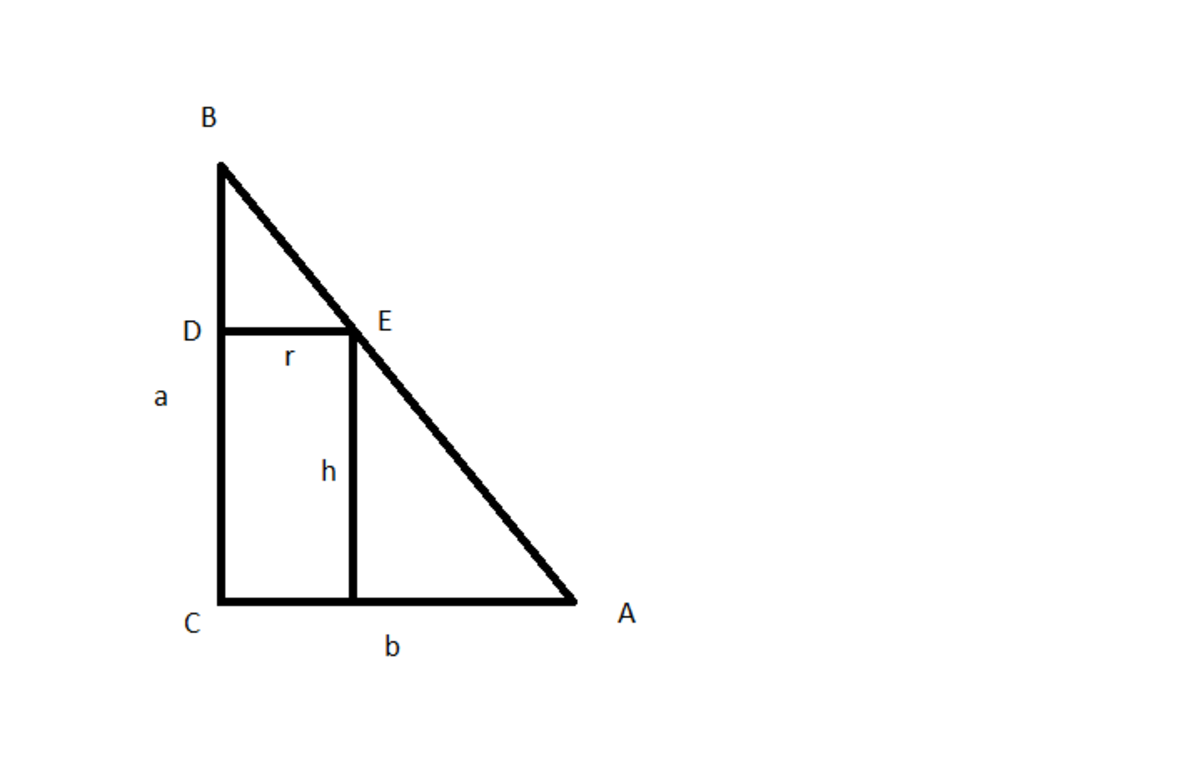

So we can take the angle <BAC and call it alpha, also we has to know the triangle BDE is similar to triangle ABC so we know

$\tan{\alpha}=\frac{a}{b}=\frac{a-h}{r}$

then we can write h as

$h=a-\frac{ar}{b}$

now we take our function to maximize, the volume of the cylinder

$V_{cyl}(r)=\pi r^{2}h=\pi r^{2}(a-\frac{ar}{b})=\pi a r^{2}-\frac{3\pi a r^{3}}{b}$

then we derivate to find a maximum or minimum point in the function, wich we can find by equaliting our derivated function to zero, saying that the slope in this point of the curve is zero to get this assumtion

$V_{cyl}'(r)=2\pi a r - \frac{3\pi a r^{2}}{b}=2-\frac{3r}{b}=0$ $r=\frac{2}{3}b$

but then you ask, how do you know that is a maximum and is not a minimum value, well we substitute this in the second derivate of our function

$V_{cyl}''(r)=2\pi a- \frac{6\pi a r}{b}$ $V_{cyl}''(\frac{2}{3}b)=2\pi a- \frac{6\pi a (\frac{2}{3}b)}{b}=2\pi a - 4\pi a=-2\pi a$

and in this way we know the value we got is a maximum, the result is negative because pi is real positive, two is also and a is a lenght of a figure, this cannot be negative.

So the maximum radius for our cylinder is $\boxed{r=\frac{2}{3}b}$