A Gloopelhopper Problem

Classical Mechanics Level 3

The most prominent, undiscovered life-form in our galaxy is the Gloopelhopper -- a giant, anaerobic, high-density slime mold that feeds on heavy metal deposits on asteroids. Gloopelhoppers can grow very massive as they hop from asteroid to asteroid. After a Gloopelhopper depletes the heavy metals on a given asteroid, it readies itself to hop to a new asteroid by roughly forming its mass into a sphere before it applies a large force on its host asteroid’s surface. The force it applies launches the Gloopelhopper from the surface of the asteroid. Of course, momentum is conserved during the launch, so large Gloopelhoppers tend to thrust their host asteroids in the opposite direction as they launch themselves (see figure).

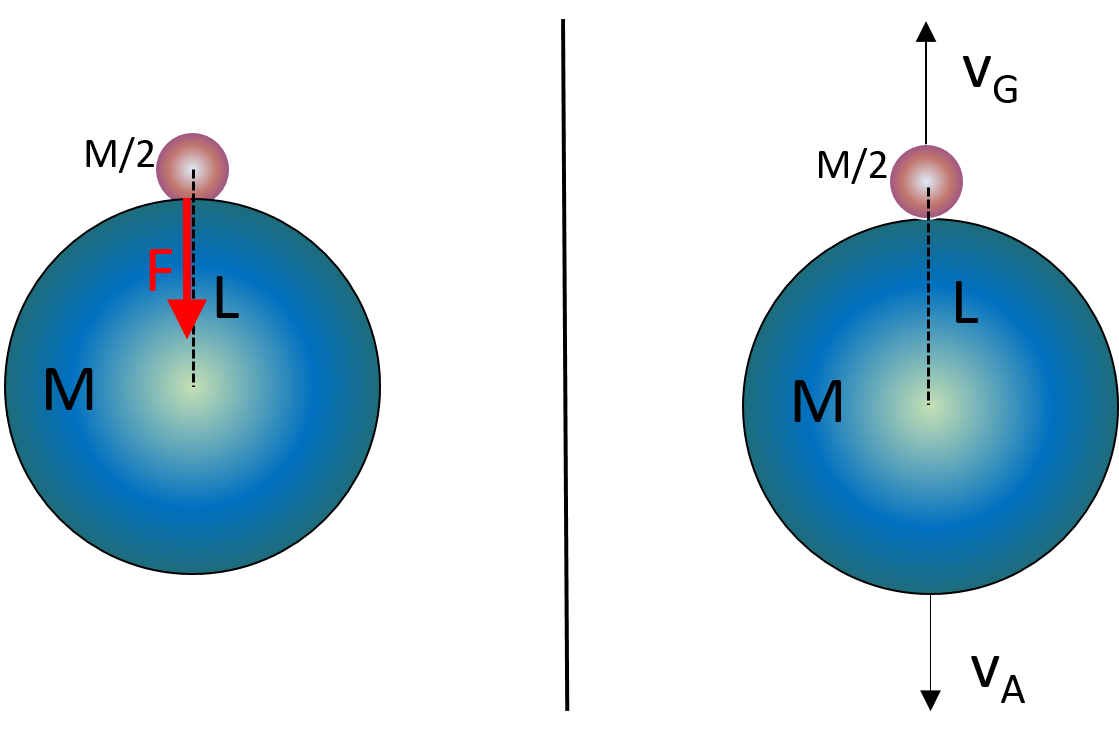
In order to successfully leave its host asteroid, a Gloopelhopper must gain enough kinetic energy during launch to escape the gravitational field of its host. Given an asteroid with mass $M$ hosting a large Gloopelhopper with mass $M/2$ , and given an initial center-to-center separation $L$ between the asteroid and the Gloopelhopper, what is the escape speed of the Gloopelhopper $v_G$ in the inertial frame where the Gloopelhopper and asteroid were initially at rest (as depicted in the figure)? Answers are expressed in terms of Newton's gravitational constant $G$ and the other given variables.

Hint : The recoil speed of the asteroid $v_A$ contributes significantly to the total kinetic energy in this problem. You can relate the asteroid’s recoil speed to the Gloopelhopper’s launch speed using conservation of momentum.

Also, you should recall that escape speed is defined specifically as the threshold speed needed for a mass to escape to infinity with no excess kinetic energy.

2 \sqrt{\frac{GM}{3L}}

\sqrt{\frac{3GM}{2L}}

3 \sqrt{\frac{GM}{L}}

\frac{1}{2} \sqrt{\frac{GM}{L}}

1 solution

Aaron Miller Staff
Jun 21, 2016

As specified in the problem, in the initial rest frame of the Gloopelhopper/asteroid system, $v_G$ is defined as the escape speed of the Gloopelhopper and $v_A$ is defined as the recoil speed of the asteroid.

Let’s start by defining kinetic energies associated with these masses and then use conservation of energy to relate them to variables given in the problem statement. Expressions for the kinetic energies are $\text{KE}_A = \frac{1}{2} M v_A^2$ and $\text{KE}_G = \frac{1}{2} \frac{M}{2} v_G^2 = \frac{1}{4} M v_G^2$ where we have used the fact that the mass of the Gloopelhopper is half of the mass $M$ of the asteroid.

We will also need to calculate the initial gravitational potential energy of the Gloopelhopper/asteroid system using the usual expression $U = -\frac{G M_1 M_2}{R}$ where $R$ is the center-to-center separation between masses $M_1$ and $M_2$ . In terms of variables given in this problem, the initial gravitational potential energy when the center-to-center separation is equal to $L$ is $U_0 = -\frac{G M \frac{M}{2}}{L} = -\frac{G M^2}{2 L}.$

We will relate the known escape speeds to Newton's constant $G$ and other givens using energy conservation. A statement of conservation of energy when there is no external work done on a system is $\text{U}_0 + \text{KE}_0 = \text{U}_f + \text{KE}_f$ where the left-hand side is the sum of initial potential and initial kinetic energies, and the right-hand side is the sum of final potential and final kinetic energies.

When massive bodies are escaping a central force like gravity, we are considering, by definition, the specific case when $\text{U}_f = \text{KE}_f = 0$ . In this case, the initial speeds appearing in $\text{KE}_0$ are called the escape speeds of the interacting bodies. In light of this definition, we can plug into the energy conservation statement both the expressions above for KE in terms of escape speeds $v_G$ and $v_A$ and the expression above for the initial gravitational potential energy $U_0$ . We find $-\frac{G M^2}{2 L} + \frac{1}{2} M v_A^2 + \frac{1}{4} M v_G^2 = 0.$ This statement relates what we are looking for, $v_G$ , to known quantities ( $M$ , $L$ , and $G$ ), and also the other unknown $v_A$ .

As mentioned in the problem’s hint, $v_A$ can be re-expressed in terms of $v_G$ using conservation of momentum. In the rest frame of the Gloopelhopper/asteroid system, the initial momentum is 0. In this frame after the Gloopelhopper is launched, the momentum is $p = Mv_A - \frac{M}{2} v_G$ which must also equal 0 because of momentum conservation. Hence, setting $p=0$ and cancelling a common factor of $M$ , $v_A = \frac{1}{2} v_G.$

Now we can use this relation to eliminate $v_A$ from the statement of energy conservation: $-\frac{G M^2}{2 L} + \frac{1}{8} M v_G^2 + \frac{1}{4} M v_G^2 = 0.$ Multiplying through by a factor of $8/M$ and after some algebra, we find $3 v_G^2 = \frac{4 G M}{L},$ so we arrive at the final answer $v_G = 2\sqrt{\frac{GM}{3L}}$ .

A Gloopelhopper Problem

1 solution

0 pending reports