A classical mechanics problem by Abhinav Jha
Classical Mechanics
Level
4
Find the greatest possible angle (in degrees) through which a deuteron is scattered as a result of elastic collision with an initially stationary proton.
source: problems in general physics.
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
tomorrow is my chem exam , yet doing this !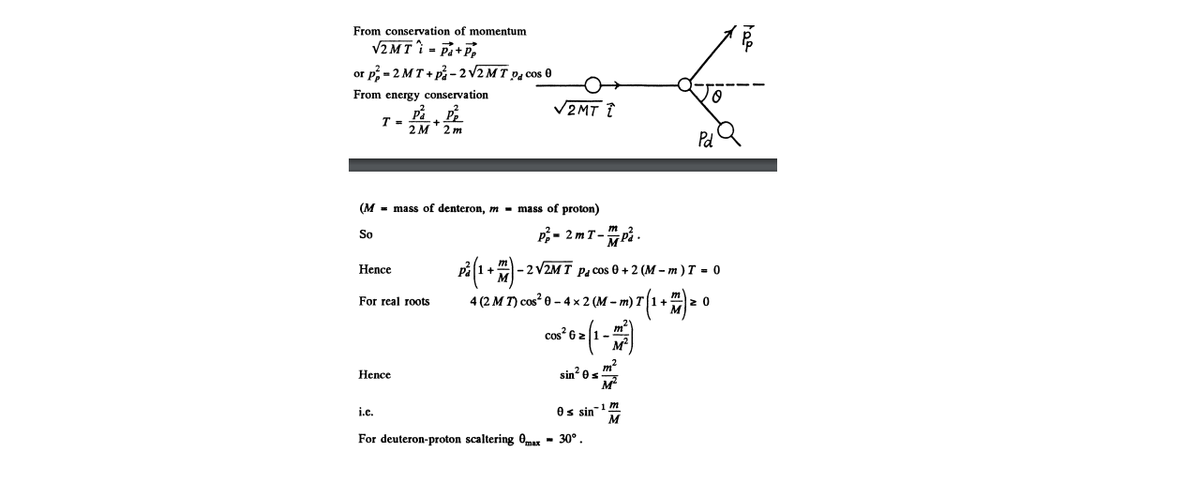 solved it like prakhar but just to give another approach !
solved it like prakhar but just to give another approach !