A classical mechanics problem by Arpita Karkera
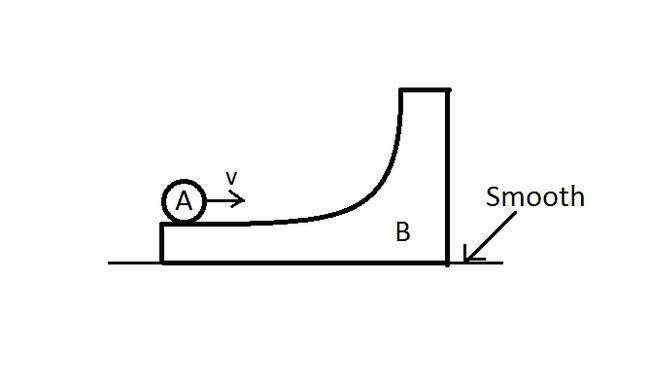 In the figure shown a ring
A
is initially rolling without sliding with a velocity
v
on the horizontal surface of the body
B
(of same mass as
A
). All surfaces are smooth.
B
has no initial velocity. Find the maximum height reached by
A
on
B
. (
g
is acceleration due to gravity).
In the figure shown a ring
A
is initially rolling without sliding with a velocity
v
on the horizontal surface of the body
B
(of same mass as
A
). All surfaces are smooth.
B
has no initial velocity. Find the maximum height reached by
A
on
B
. (
g
is acceleration due to gravity).
Answer comes out as b g a v 2 where a and b are coprime integers
What is the value of a + b ?
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Please mention that mass of ring and wedge is same.
Nice problem, but do mention that a , b are coprime integers.
Excuse me but at the top most point, how will the ring be still rotating? The 2 1 I ω 2 term will be zero, since the ring has no velocity perpendicular to the surface.
The answer should be 4 g 3 v 2
Log in to reply
Since all the surfaces are smooth, friction will not act on the ball. So, its angular speed will remain constant (net torque is zero).
Due to friction the ring still doing pure rolling
But how is the velocity of plank and ring same at top most point
Will angular momentum conserved
And linear momentum is not conserved in vertical direction due to gravity right
When the A will be at the highest position, its vertical velocity will be zero and horizontal velocity will be equal to that of B. (Let mass of each body be m)
Linear momentum will be conserved in horizontal direction,
m v = m v 1 + m v 1
v 1 = 2 v
Total mechanical energy is conserved,
2 1 I ω 2 + 2 1 m v 2 + 0 = 2 1 I ω 2 + 2 1 m v 1 2 + 2 1 m v 1 2 + m g h
v 2 = 2 v 1 2 + 2 g h
v 2 = 2 v 2 + 2 g h
v 2 = 4 g h
h = 4 g v 2
a=1 and b=4 a+b=5