Shape made by the farthest points on a ramp
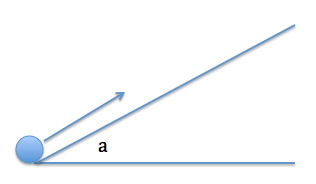
A frictionless ramp makes an angle to the horizontal, and that angle is adjustable between 0° and 90°.
You slide a mass up the ramp many times, giving it the same initial velocity each time, but setting the ramp to a different angle each time. You note the coordinates of the mass (in the 2D plane of the ramp) each time it reaches its farthest point along the ramp before sliding back down.
If you plot the coordinates you noted for each the trials together on a 2D plane, what shape will those points describe?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The simplest way to determine the locus of points described by the highest point the mass reaches for different ramp angles is using the principle of Conservation of Energy.
Since the mass has the same velocity v every time, the mass begins its trip up the ramp with total energy
E 0 = 2 1 m v 2
since its energy is entirely kinetic energy (KE). I have chosen the bottom of the ramp to be the reference point where the gravitational potential energy (GPE) is zero.
At the highest point the mass reaches when it comes to a stop, the KE has entirely transformed into GPE (thanks to the frictionless nature of the ramp), so at the end
E 1 = m g h
where g is the local acceleration due to gravity, and h is the height of the mass at its highest point. The principle of Conservation of Energy states that the total energy remains the same, so
E 0 = E 1
2 1 m v 2 = m g h
Solving for h ,
h = 2 g v 2
The height of the mass, as can be seen in this last expression, is independent of the angle of the ramp a , and both v and g are constant from trial to trial. That means that regardless of the angle, the mass rises to the same maximum height every time. If all the points in our locus have the same height, then the shape they describe must be a horizontal line .