Slide down and go the distance
What should be the height H in meters so that the ball of mass 1 k g reaches the point A ?
Take g = 1 0 m / s 2 .
- There is no friction in this system.
- The ball is not rolling it is sliding.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
This one was easy.
Nicely put together solution. Question should have stated that the ball leaves the ramp horizontally - not obvious when viewed on a smartphone!
Log in to reply
Thanks. Yes, the question should have mentioned that the ball leaves the ramp horizontally, else it cannot be solved.
Relevant wiki: Understanding the work-kinetic energy theorem
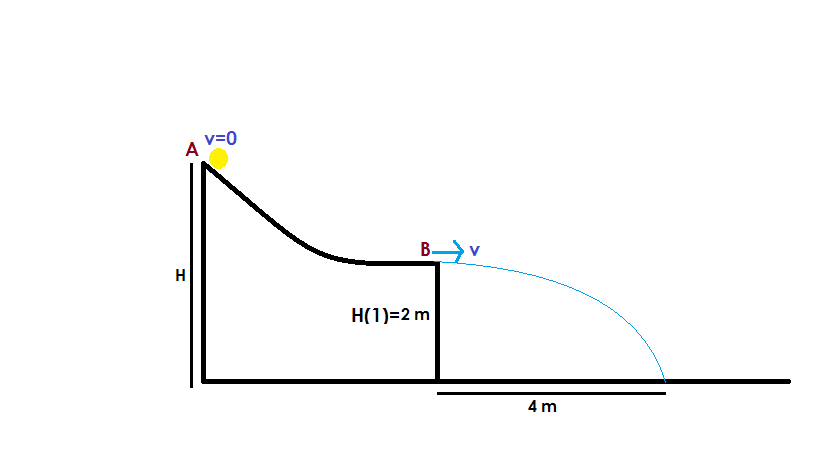 Applying Work-Energy Theorem between points A and B
m
g
H
v
2
+
2
g
H
1
=
m
g
h
1
+
2
1
m
v
2
=
2
g
H
(
1
)
Since particle strikes the ground at a horizontal distance of 4 m ,
v
×
g
2
H
1
v
2
=
d
=
2
H
1
g
d
2
(
2
)
Substituting value of
v
2
from equation (2) in equation (1) , We get
2
g
H
=
2
H
1
g
d
2
+
2
g
H
1
Putting
H
1
=
2
m
,
d
=
4
m
, and
g
=
1
0
m
/
s
2
,
we get,
H
=
4
m
.
Applying Work-Energy Theorem between points A and B
m
g
H
v
2
+
2
g
H
1
=
m
g
h
1
+
2
1
m
v
2
=
2
g
H
(
1
)
Since particle strikes the ground at a horizontal distance of 4 m ,
v
×
g
2
H
1
v
2
=
d
=
2
H
1
g
d
2
(
2
)
Substituting value of
v
2
from equation (2) in equation (1) , We get
2
g
H
=
2
H
1
g
d
2
+
2
g
H
1
Putting
H
1
=
2
m
,
d
=
4
m
, and
g
=
1
0
m
/
s
2
,
we get,
H
=
4
m
.
@Prakhar Bindal Check this one
If this involved energy systems then why is it given in kinematics 2d?
Let the velocity the ball leaving the ramp be v ms − 1 . Since the ball leaves horizontally, the horizontal and vertical components of v are v x = v and v y = 0 respectively.
The time t taken for the ball to drop a distance of h is given by:
h 2 ⟹ t = v y t + 2 1 g t 2 = 0 + 2 1 ( 1 0 ) t 2 = 5 2 s
In time t , the horizontal distance travelled by the ball d is given by:
d ⟹ v x v = v x t = t d = 4 × 2 5 = 4 0 ms − 1
When the ball drop from H to h , its potential energy is converted to kinetic energy as follows:
m g ( H − h ) ⟹ H = 2 1 m v 2 = 2 g v 2 + h = 2 ( 1 0 ) 4 0 + 2 = 4 m