A classical mechanics problem by Godwin Tom George
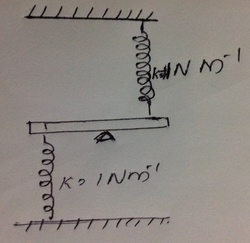
A uniform rod of length 2m and mass 6KG is pivoted at it's centre.It is held in position by a system of springs as shown in the figure.If the rod is slightly turned and released then time period of oscillation in seconds is.
K=1N/m
The answer is 6.2857143.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First of all, Clearly, since the use of springs is linearly involved, we can derive that the motion shown by the bar, is a an SHM. Now, in a Simple Harmonic Motion, the total energy of the body remains constant throughout the motion. So, what I'm going to do, is to take an instant, and differentiate the total energy of the system with respect to displacement, and equate it to 0 .
Let at an instant, the extension in both the springs is ′ x ′ each, as the situation is symmetrical. Let, the mass of the body be ′ M ′ and it's length be ′ l ′ . Let at this instant the angular velocity of the body be ω . So, total energy at this instant is : T o t a l E n e r g y ( E ) = 2 1 K x 2 + 2 1 K x 2 + 2 1 I ω 2 , where I is the moment of inertia of the bar.
Differentiating this expression with respect to ′ x ′ : d x d E = 0 ⇒ d x d ( 2 1 K x 2 + 2 1 K x 2 + 2 1 I ω 2 ) = 0 ⇒ d x d ( K x 2 ) + d x d ( 2 1 I ω 2 ) = 0 ⇒ d x d ( − K x 2 ) = d x d ( 2 1 I ω 2 ) ⇒ − 2 K x = 2 1 d x d ( 1 2 M l 2 ω 2 ) ⇒ − 4 K x = 1 2 M l 2 d x d ( ( 2 l ) 2 v 2 ) ⇒ − 4 K x = 1 2 M l 2 l 2 4 d x d ( v 2 ) ⇒ − 4 K x = 3 M 2 v d x d v
But, v d x d v = a
So, ⇒ − 6 K x = M a ⇒ F = − 6 K x
Clearly , this is an SHM with spring factor K ′ = 6 K
Now, time period for an SHM (T) = 2 π S p r i n g F a c t o r I n e r t i a l F a c t o r Here, Inertial factor is the mass of the body, and the spring factor is K ′ = 6 K
So, T = 2 π K ′ M ⇒ T = 2 π 6 K 6 ⇒ T = 2 π 6 6 ⇒ T = 2 π s e c o n d s = 6 . 2 8 s