A classical mechanics problem by Miraj Shah
Consider a body, attached to a string of length r , to be initially at rest in the vertical plane. It can be proved that if we give the body an initial velocity of v > 5 g r , then, the body can make complete revolutions in the vertical plane about the point of suspension.
Let us consider that the body, initially at rest, is given a velocity v < 5 g r . If at this value of v the body eventually hits the point of suspension then we can write:
v 2 = ( a + b ) g r .
Find a × b .
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I'm not very good at kinematics - how do you arrive at equation 1? Thanks.
Log in to reply
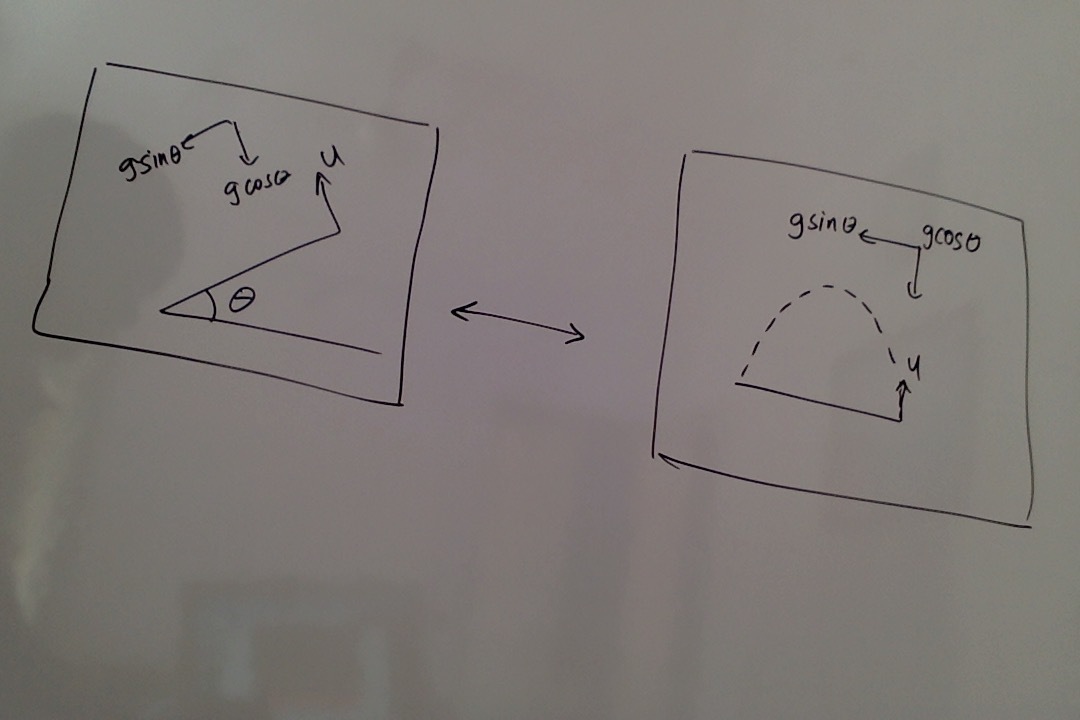
Refer to the figure above.
We know that the formula for time of flight in general for a body performing projectile motion is t = a y 2 u y .
Here u y = Magnitude of velocity of the body in the vertical direction and
a y = Magnitude of acceleration of body in the vertical direction
As you can see from the figure above, here u y = u and a y = g c o s θ . Plugging in the values we get t = g c o s θ 2 u .
If you still have any doubt or problem regarding this or any other part of the solution feel free to ask.
And sorry for replying to your question a bit late!
Log in to reply
Oh.. thanks! I tried to make u into its velocity components rather than g and wondered how you arrived at a division by cos θ . This helped me a lot.
let us consider the string to become slackened at an angular position \(\theta) measured from horizontal in anticlockwise direction.
at this point, tension in string is zero.
thus \(mgsin\theta=\frac{mv^{'2}}{r}\) where v ′ is the velocity at point of slackening.
thus v ′ = g r s i n θ
from this point onwards, the path of ball is parabolic with general equation being,
y = x c o t θ − 2 v ′ 2 s i n 2 θ g x 2
plugging in the values in this equation, − 2 s i n 4 θ = 2 c o s 2 θ s i n 2 θ − c o s 2 θ
convert everything in terms of sine and obtain s i n θ = 3 1
now by energy conservation the relation between v a n d v ′ is found to be v 2 = 2 g r + 3 g r
therefore a is 2 and b is 3.
But I know the general equation has tan theta as the coefficient of x so can you please explain
It's an hc verma example question
Volume 1 page 130
After the instant, when tension in the string becomes zero, the body does not perform circular motion but instead follows a parabolic path. Let the velocity of the body at the instant tension in the string becomes zero, be u as shown in the figure. Let the time taken from this instant to reach the point of suspension be t .
Therefore,
t = g cos θ 2 u .... ( 1 )
Also, at the exact instant when the tension in the string becomes zero, we can write the equation of motion as follows:
Net Force towards Centre = r m u 2
⇒ m g sin θ = r m u 2
⇒ u 2 = g r sin θ .... ( 2 )
Now, we also know that the horizontal component of u is u x = u sin θ
Therefore,
( u x ) ( t ) = Net displacement in the horizontal direction.
( u sin θ ) ( t ) = r cos θ
⇒ 2 u 2 sin θ = g r cos 2 θ ....(from equation ( 1 ) )
⇒ 2 g r sin 2 θ = g r cos 2 θ ....(from equation ( 2 ) )
⇒ tan θ = 2 1 ⇒ sin θ = 3 1 ⇒ u 2 = 3 g r
Now that we know the value of u 2 we can use the Law of Conservation of Energy to find v 2
On calculating we get:
v 2 = g r ( 2 + 3 )
Therefore, a b = 6