Maximum velocity of the block!
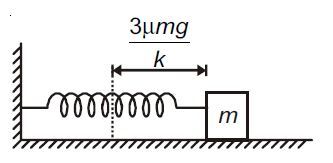 A spring of spring constant
k
connected to a block of mass
m
is placed on a rough horizontal surface having coefficient of friction
μ
. The spring is given initial elongation
k
3
μ
m
g
and the block is released from rest. For the subsequent motion, the maximum speed of the block is?
A spring of spring constant
k
connected to a block of mass
m
is placed on a rough horizontal surface having coefficient of friction
μ
. The spring is given initial elongation
k
3
μ
m
g
and the block is released from rest. For the subsequent motion, the maximum speed of the block is?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
But i am getting 2 μ g k 2 m
How do you make these diagrams while posting physics questions? @Nishant Rai
Once the spring force is equal to the friction force, friction will absorb
K.E.and so the velocity will then go on decreasing.
S
o
V
m
a
x
will take place when spring and friction forces are equal.
At this point, that is at elongation of
X
v
m
a
x
,
k
∗
X
v
m
a
x
=
μ
∗
m
∗
g
.
And the block will stil lhave P.E. of
k
∗
X
v
m
a
x
2
=
k
(
μ
∗
m
∗
g
)
2
.
.
.
(
1
)
So the P.E. lost in friction PLUS converted to K.E.
=
I
n
i
t
i
a
l
P
.
E
.
−
P
.
E
.
l
e
f
t
a
t
V
m
a
x
g
i
v
e
n
i
n
(
1
)
=
2
1
∗
k
∗
{
(
3
μ
m
g
)
2
−
(
μ
m
g
)
2
}
=
k
4
∗
(
μ
m
g
)
2
.
P.E . absorbed by friction PLUS that converted to K.E.
=
μ
m
g
∗
k
{
3
μ
m
g
}
+
2
1
m
∗
V
m
a
x
2
=
k
3
∗
(
μ
m
g
)
2
+
2
1
m
∗
V
m
a
x
2
=
k
4
∗
(
μ
m
g
)
2
.
V
m
a
x
=
2
μ
g
k
m
This is how I would like to explain
N
i
s
h
a
n
t
R
a
i
′
s
idea.
You can directly use fact of SHM , that
V
m
a
x
=
A
ω
k
A
=
3
μ
m
g
−
μ
m
g
=
2
μ
m
g
ω
=
m
k
V
m
a
x
=
k
2
μ
m
g
×
m
k
=
2
μ
g
k
m
but the amplitude here is not constant to apply the formula as you said of shm,isnt it..
(Apply conservation of Energy.)
(Note that a body attains it's maximum speed when all the external forces acting on it gets balanced.)
⇒ k x = μ m g where x is the compression in the spring at the time of maximum velocity of the block.