Lift the second Block!
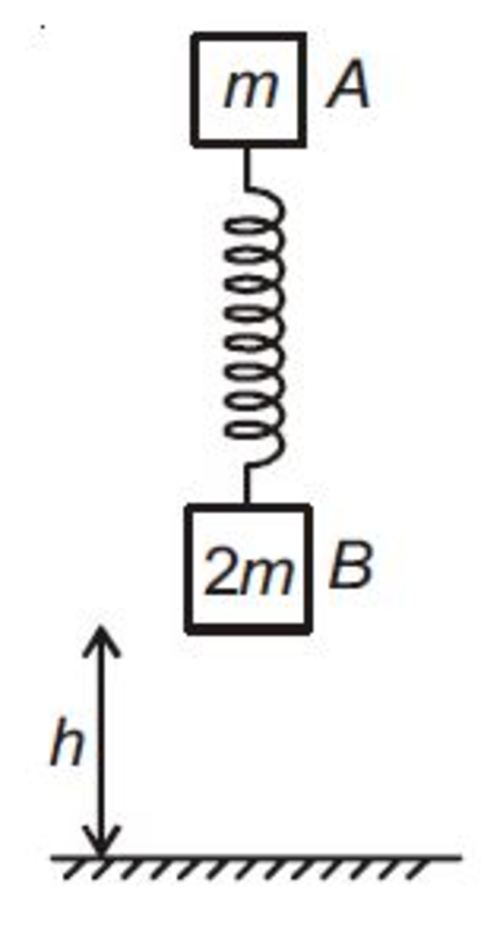 The system of blocks must be released from
h
>
k
n
m
g
with the spring unstretched so that after perfectly inelastic collision (
e
= 0) with ground,
B
may be lifted off the ground. Find the least possible value of
n
. (
k
is spring constant).
The system of blocks must be released from
h
>
k
n
m
g
with the spring unstretched so that after perfectly inelastic collision (
e
= 0) with ground,
B
may be lifted off the ground. Find the least possible value of
n
. (
k
is spring constant).
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Why is it m g (h-x) and not m g (x+h)? When the mass 2m reaches the surface, 2m and m have both moved h distance from their initial position. After that , 2m will stop but m will continue moving downwards due to the kinetic energy and would compress the spring by an additional distance x. So shouldn't it be h+x?
∣ x i ∣ = maximum compression of spring ... x i < 0
∣ x f ∣ = maximum elongation of spring ... x f > 0
In order for mass B to leave the ground ... k x f = 2 m g ...This is the first constraint.
Relationship between x f and x i from conservation of energy (all of the energy of block B is lost in the inelastic collision) ... 0 . 5 k x i 2 = 0 . 5 k x f 2 + m g ( x f − x i ) ... This is the second constraint.
Relationship between x i and h from conservation of energy ... 0 . 5 k x i 2 = m g ( h − x i ) ... This is the third and final constraint.
These three constraints solve the problem. To finish, combine the first two constraints to eliminate x f and you will get 0 . 5 k x i 2 = k 4 ( m g ) 2 − m g x i and then set this equal to the third constraint and you will get h = k 4 m g which is the minimum value of h.
u shouldn't have solved the quadratic, u should have equated ur equation 1 and the equation below, using this 0 . 5 k x i 2 a n d m g x i would cancel out
Log in to reply
Ah good catch, I did the algebra the hard way. I edited the answer, thanks Tanishq.
k x = m g
⇒ x = k 2 m g
Initial energy of A (only) E 0 = m g h
Energy at final position (spring stretched a distance x E f − m i n i m u m = 2 k x 2 + m g x = 2 ⋅ k 2 m 2 g 2
m g h = k 4 m 2 g 2
⇒ h = 4 ⋅ k m g
Check mine!
Since there is e=0, B does not contribute to lifting it up. Only spring energy has to lift it up. After the spring is compressed, A moves up with velocity till its up motion is stopped. So question of lifting A up does not arise, if before that B is lifted up as in our case. So if spring is extended by x with reference to up moving A, so that the spring forces B up, with the force of B's weight, B is just lifted. That implies 2mg=xk. That is x = k 2 m g . That means, A is( h - x) high at that point. Implies spring must have stored P.E. energy lost by A. But P.E. lost = mass*(gravity acc.) *( height lost ) =Energy gained by the spring due to A. Note:-During this proses, one end of the spring is as if fixed to the ground.
1 ∗ m ∗ g ∗ ( h − x ) = 2 1 ∗ k ∗ x 2 . ⟹ m g ( h − k 2 m g ) = 2 1 ∗ k ∗ ( k 2 m g ) 2 . S o l v i n g h = k 4 m g = k n m g , ⟹ n = 4