A classical mechanics problem by Rishabh Deep Singh
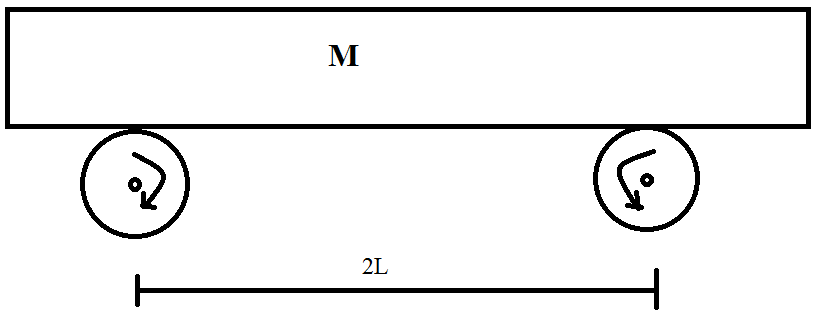
Two wheels which are rotated by some external source with constant angular velocity ( ) in opposite directions as shown in the figure above. A uniform plank of mass is placed symmetrically. The friction coefficient between each wheel and the plank is . Find the frequency of oscillation, when the plank is slightly displaced along its length ( ) and relapsed.
Details and Assumptions :
-
.
-
Neglect end effect caused by extra length of plank.
The answer is 0.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
I f t h e p l a n k i s d i s p l a c e d b y x t o w a r d s r i g h t t h e n . L e t N 1 , N 2 a n d f 1 , f 2 a r e n o r m a l a n d f r i c t i o n F o r c e s a t P o i n t s A a n d B . B y f o r c e b a l a n c i n g N 1 + N 2 = M g − − − − − − − − ( 1 ) B y t o r q u e b a l a n c i n g a b o u t p o i n t A M g ( L + x ) = N 2 . ( 2 L ) − − − − − − − − ( 2 ) U s i n g e q u a t i o n ( 1 ) a n d ( 2 ) N 1 = 2 M g − 2 L M g x a n d N 2 = 2 M g + 2 L M g x S o f 1 = μ N 1 = μ ( 2 M g − 2 L M g x ) a n d f 2 = μ N 2 = μ ( 2 M g + 2 L M g x )
f 2 − f 1 = M a μ ( 2 l 2 M g x ) = M a = − d t 2 d 2 x . M d t 2 d 2 x = − l μ g x C o m p a r i n g w i t h d t 2 d 2 x = − ( ω ) 2 . x ω = l μ g T i m e p e r i o d T = ω 2 π T = 2 π μ g l F r e q u e n c y ( ν ) = 2 π 1 l μ g ν = 2 π 1 1 1 . π 2 = 2 π π = 0 . 5