A classical mechanics problem by Rishabh Tiwari
A particle is moving along x -axis with a constant acceleration of − 2 ms − 2 . The particle leaves the origin with a velocity of 5 ms − 1 . Determine the distance (in m ) travelled by the particle during the third second of its motion.
The answer is 0.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Thank you :-) Nice solution (+1)! You loved it but you didn't liked it :(
Nice approach! (+1)!
Log in to reply
Thanks :):)
Log in to reply
Did you appeared for jee this year or you are in 11th ?
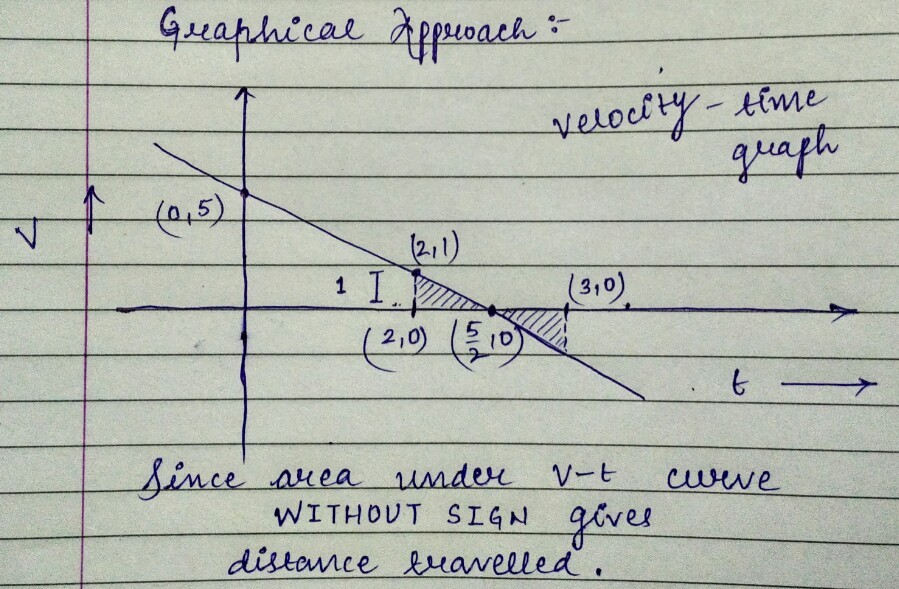
Let's see when the particle comes to rest ,
From v = u + at ,
0 = 5 − 2 t
⇒ t = 2 . 5 s ,
Hence, the particle changes its direction of motion at t = 2 . 5 s , so we cannot directly use the formula of distance travelled in n t h sec. Therefore we will calculate distance travelled from t = 2 to t = 2 . 5 & from t = 2 . 5 to t = 3 separately !
Now , we use x = u t + 2 1 a t 2
For displacement in t = 2 to t = 2 . 5 , we subtract the displacement at t = 2 from displacement at t = 2 . 5 :-
x 1 = 5 ⋅ ( 2 ) − 4 ⇒ x 1 = 6 m ....(disp. in t = 2s)
x 2 = 5 ⋅ ( 2 . 5 ) − 6 . 2 5 ⇒ x 2 = 6 . 2 5 m ....(disp. in t = 2.5s)
Required displacement = x 2 − x 1 = 0 . 2 5 m .......................... ( 1 )
Now our half work is done, For t = 2 . 5 to t = 3 , we have :
u = 0
a = + 2
t = 0 . 5
Putting these values in
x = u t + 2 1 a t 2
We get x = 0 . 2 5 m ...................... ( 2 )
Adding ( 1 ) & ( 2 ) we get net displacement in 3rd second as x = 0 . 5 m .
Please feel free to comment & correct me if I am wrong & would really appreciate if someone posts a better & short solution. Thank you .
Use graph to under stand the solution of this problem,make a velocity vs time graph,,,and draw the graph of this problem v=5-2t And are under the line of eqn. at t=2to t=3 So finally ur and is o.5.....

Notice that the particle have initial velocity towards + x axis and acceleration towards − x axis
If we apply the direct formula to calculate the Displacement in n t h second , we get
S n = u + 2 a ( 2 n − 1 ) ⟹ S 3 = 5 − 2 2 ⋅ ( 5 ) = 0
Now to calculate the distance , we have to use laws of motion
First Let's calculate the time when velocity of the particle is 0
v = u + a t ⟹ 0 = 5 − 2 ⋅ t t = 2 . 5 Seconds
Total Distance traveled by the particle ( S ) will be
S = 2 ( S 2 . 5 − S 2 ) S = 2 ( 5 ⋅ 2 . 5 − 2 1 ⋅ 2 ⋅ 6 . 2 5 − 5 ⋅ 2 + 2 1 ⋅ 2 ⋅ 4 ) S = 2 ( 1 2 . 5 − 6 . 2 5 − 1 0 + 4 ) S = 0 . 5 m
Nice problem , i loved it :)