The Time-keeper
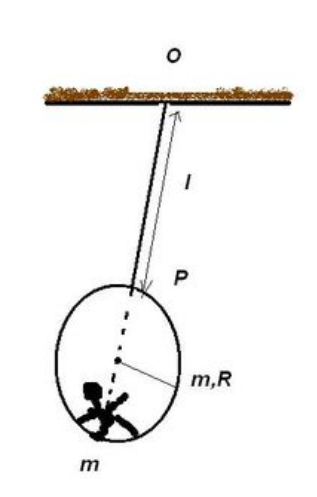
A man sits on the inner side of a hollow sphere and measures the seconds as they pass. Find the time (in ) he measures during one oscillation of the pendulum.
Details and Assumptions
- Length of string is
- Radius of sphere is
- String is attached at point and man sits diametrically opposite to this point.
- Masses of both man and sphere are same.
-
The man doesn't slip on the sphere ie., he sits at the same point on the sphere.
-
Assume the figure at the bottom of the sphere to be the man.
-
The oscillations take place in uniform gravitational field where SI units.
This problem is part of the set innovative problems in mechanics .
The answer is 3.3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
the time period of a physical pendulum is given by 2 π m g d I ---------------------- i
we will not go into how this is got. one can find the derivation in any good mechanics book.
now assuming that the reader knows the theorems of inertia(ie.,parallel axis theorem,perpendicular axis theorem,pappus theorem), i will claim that the moment of inertia of the composite system about axis of oscillation O IS 6 3 4 m R 2 + 2 m l 2 + 6 m l R
d is the distance of centre of mass from the point of oscillation O
this is easily computed to be l + 2 3 R
now substituting in i ,
T = 2 π 6 g ( 3 R + 2 l ) 3 4 R 2 + 1 2 l 2 + 3 6 l R
from here, T=3.31 seconds
thus,the man has counted 3 seconds