Rolling all the way down

Classical Mechanics Level 4

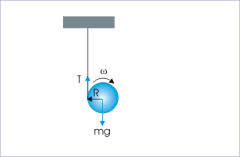
A hollow sphere has a light rope wound over it. The end of the rope is attached to a rigid support which is at a height h h from the surface of the earth, It acquires the same velocity just before touching the ground as that acquired by a free falling body under gravity from a height h ′ h' from the surface of the earth.If R e R_{e} is the radius of the earth, what is the value of R e [ 3 h ′ − 5 h ] R_{e} [\dfrac{3}{h'} - \frac{5}{h} ] ?

Details and Assumptions :

  • Radius of sphere is very much smaller than radius of earth

  • Consider the variation of acceleration due to gravity with height as both h h and h ′ h' are quite large

  • The rope doesnt slip on the sphere.


The answer is 2.

Rohith M.Athreya by Rohith M.Athreya , 22, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Rohith M.Athreya
Feb 27, 2016

now since there is no slipping between rope and sphere, acceleration of sphere will be constrained to being acceleration of unwinding of rope.

by using angular analogue of newton's second law of motion, T r = I @ r Tr=I@r here I is 2 m r 2 3 \frac{2mr^{2}}{3} and @ is the angular acceleration of sphere.

moreover applying newton's second law to the sphere as far as translation is concerned, m g − T = m @ r mg-T=m@r

from this we get that the acceleration of sphere is 3 g / 5 3g/5

however,here g is G M ( R + x ) 2 \frac{GM}{(R+x)^{2}} where G is universal gravitational constant,M the mass of the earth and R its radius

now, negative acceleration of x is the acceleration of sphere.

− v d v d x \frac{-vdv}{dx} = G M ( R + x ) 2 =\frac{GM}{(R+x)^{2}}

integrating we get, v 2 = 6 G M h 5 R ( R + h ) v^{2}=\frac{6GMh}{5R(R+h)}

also for a free falling body falling from height h' ,

by energy conservation.

v 2 = 2 G M h ′ R ( R + h ′ ) v^{2}=\frac{2GMh'}{R(R+h')}

since question states that both these velocities are equal,

2 G M h ′ R ( R + h ′ ) = 6 G M h 5 R ( R + h ) \frac{2GMh'}{R(R+h')}=\frac{6GMh}{5R(R+h)}

2 h h ′ = R [ 3 h − 5 h ′ ] 2hh'=R[3h-5h']

dividing both sides by hh' ,

R e [ 3 h ′ − 5 h ] = 2 R_{e} [\dfrac{3}{h'} - \frac{5}{h} ]=2

2 Helpful 0 Interesting 0 Brilliant 0 Confused

Its really a nice problem and solution Keep posting

Prakhar Bindal - 5 years, 3 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...