Spring-back to your basics!
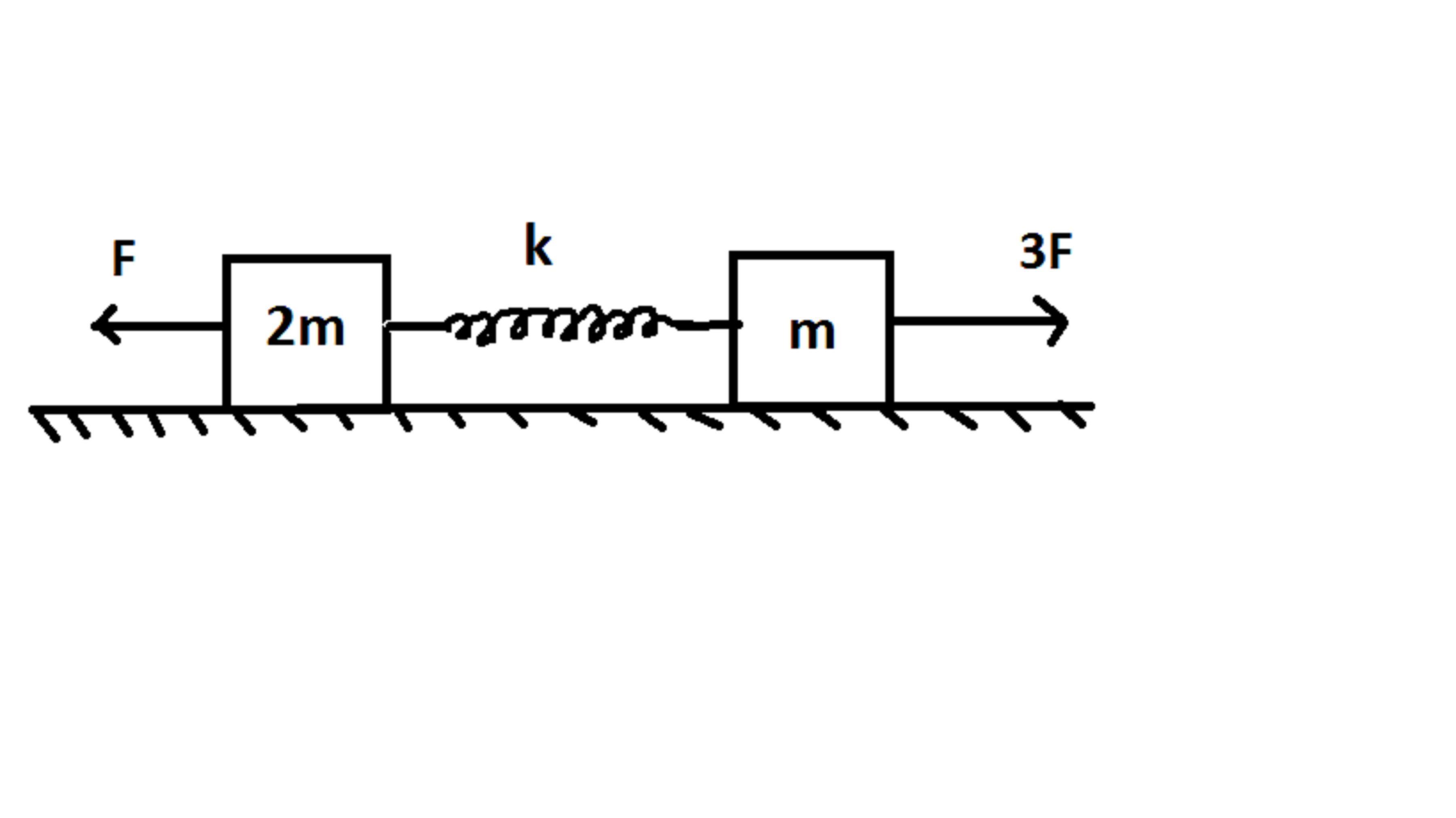
In the figure shown above. the surfaces are friction-less. Find the Maximum extension in the spring(in meters ) , if the blocks are initially at rest and the spring is initially in its natural length.
Details and Assumptions :
∙ m = 5 k g
∙ F = 3 0 N
∙ k = 7 0 0 N m − 1
This question is part of the set Best of Me
The answer is 0.2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
How did you solve this equation if there are 2 unknowns in 1 equation?
Very neat and nice! +1
I just jumbled,how the Pseudo fore {2F/3} is calculated;please explain it. Thank You
Log in to reply
This is from acceleration of system x mass of right side
Good job! Good job!
short than satvik pandey Sit in frame of m and apply pseudo forces on 2m ((force on right side=F+2m(3F/m)=7F)) and ((force on left=kx+2m(kx/m)=3kx)) just equate work done(because max extension is when 2m is at rest with respect to small m) 7Fx=3/2k{x}square x=14F/3k=0.2
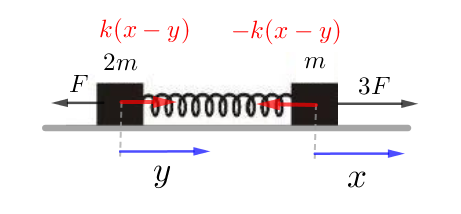
Apply Newton's 2nd law on each body to obtain*:
m x ¨ 2 m y ¨ = = 3 F − k ( x − y ) ( 1 ) − F + k ( x − y ) ( 2 )
Combine the equations as follows, ( 1 ) − 2 1 ( 2 ) , and apply the variable change l = x − y to obtain:
m l ¨ = − 2 3 k l + 2 7 F ( 3 )
The general solution to equation ( 3 ) is l ( t ) = A sin ( ω t − φ 0 ) + 3 k 7 F where A and φ 0 are constants and ω = 2 m 3 k .
Use the initial conditions l ( 0 ) = 0 and l ˙ ( 0 ) = 0 to find the value of these constants:
l ( 0 ) = A sin ( ω ⋅ 0 − φ 0 ) + 3 k 7 F = 0 ⟹ φ 0 = arcsin 3 k A 7 F l ˙ ( t ) = ω A cos ( ω t − φ 0 ) ⟹ l ˙ ( 0 ) = ω A cos ( − φ 0 ) = 0 ⟹ φ 0 = 2 π ⟹ A = 3 k 7 F
The maximum value of l ( t ) is reached when sin ( ω t − φ 0 ) = 1 , that is:
l m a x = A + 3 k 7 F = 3 k 1 4 F = 0 . 2 0 0 m
*As you may already know, a dot over a variable indicates the derivative with respect to t , and two dots, the second derivative.
Let us consider two blocks and the spring as a system.
Net external force acting on the system is 3 F − F
So by Newton's second law acceleration of the CoM of the system ( a c m is
a c m = 3 m 2 F
Consider a reference frame which is moving with the CoM of the system as it is a non-inertial frame of reference so we have to include Pseudo force on the blocks.
Let the displacement of block of mass m be x towards right and that of 2m be y towards left as seen from the CoM of the system.
Work done by all the e x t e r n a l forces on the right block is ( 3 F − 3 2 F ) x (Note: Here, 3 2 F is pseudo force acting on the right block in left direction.)
Work done by all the e x t e r n a l forces on the left block is ( 3 4 F + F ) y
This work done is equal to the change in the potential and kinetic energy of the system. If the extension has to be maximum then velocities of the block wrt CoM of the system should be zero. So the final kinetic energy of the system is zero.
So
( 3 F − 3 2 F ) x + ( 3 4 F + F ) y = 2 k ( x + y ) 2
On solving the equation and putting the values we get x + y = 0 . 2 .