Mechanics
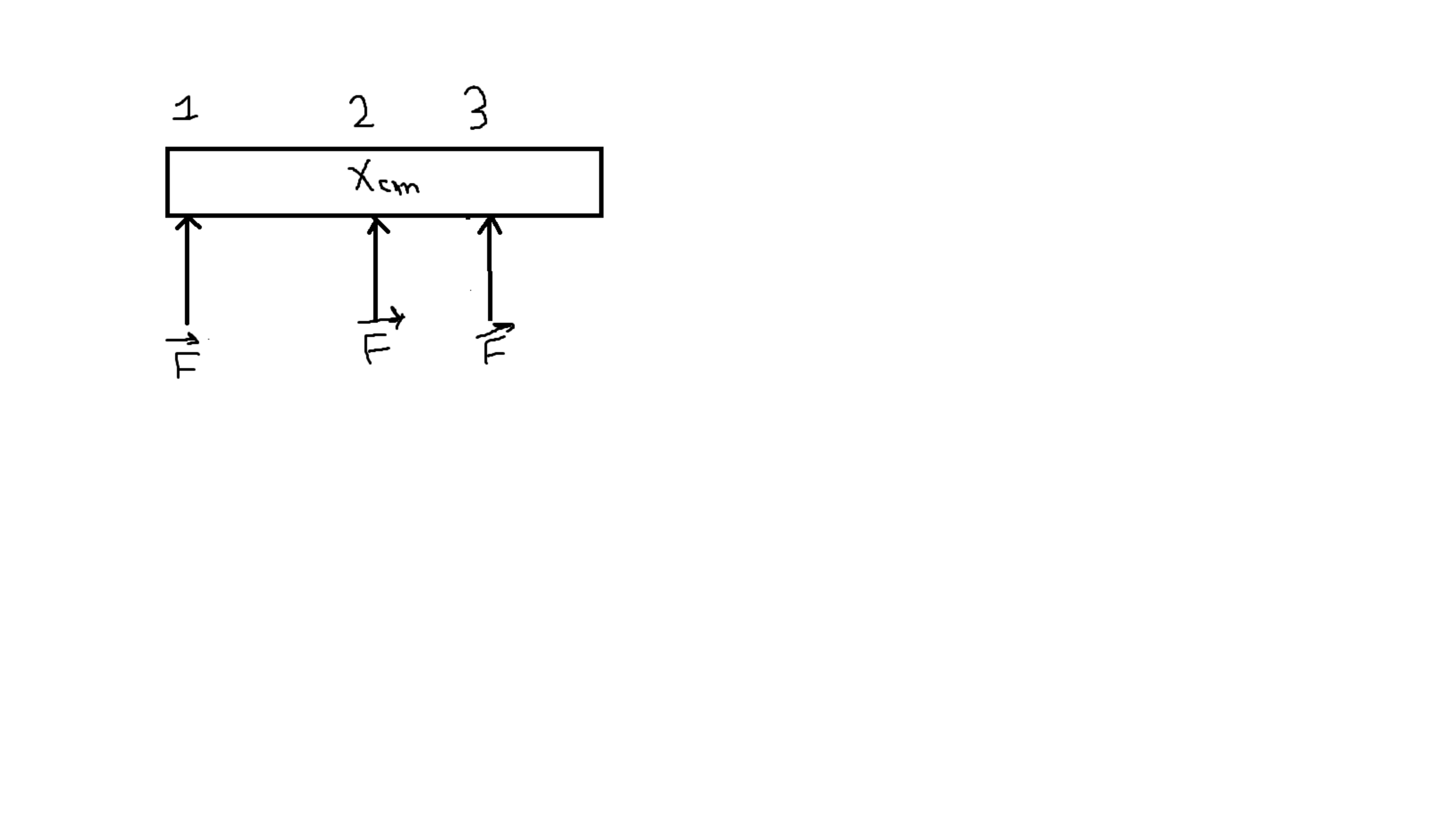
A uniform rod initially at rest on a frictionless and horizontal surface is pushed by a force of magnitude . You may assume that the push is instantaneous.
At which of the following locations will the force produce an acceleration of the center of mass with the largest magnitude?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The motion of the center of mass of a rigid object follows Newton's 2nd law: F(External) = m*acceleration of centre of mass. - During the time interval of the push, the forces acting on the object are the pushing force F and the gravitational and normal forces which add to zero; therefore {∑F external = F }........................................................ {l a l = lFl / m .} we conclude that the acceleration of the center of mass of the object is independent of the point of application of the force. For translational motion, i.e., for the description of the motion of the center of mass of an object we will look at the sum of the external forces acting on the object and not at the point where the forces are applied.
The point of application of the force is relevant to the description of the rotational motion of a rigid body.
If the rod is pushed at point 1 it will translate and at the same time rotate clockwise about the center of mass, whereas pushing it at point 3 it will translate and rotate counterclockwise. Pushing the object at point 2, the center of mass, the object will only translate. For the three cases the acceleration of the center of mass is the same because the same external force is being applied to the object. In contrast, the angular acceleration is different in the three cases and it depends on the point of application of the external forces.