That was another close call!

Classical Mechanics Level 3

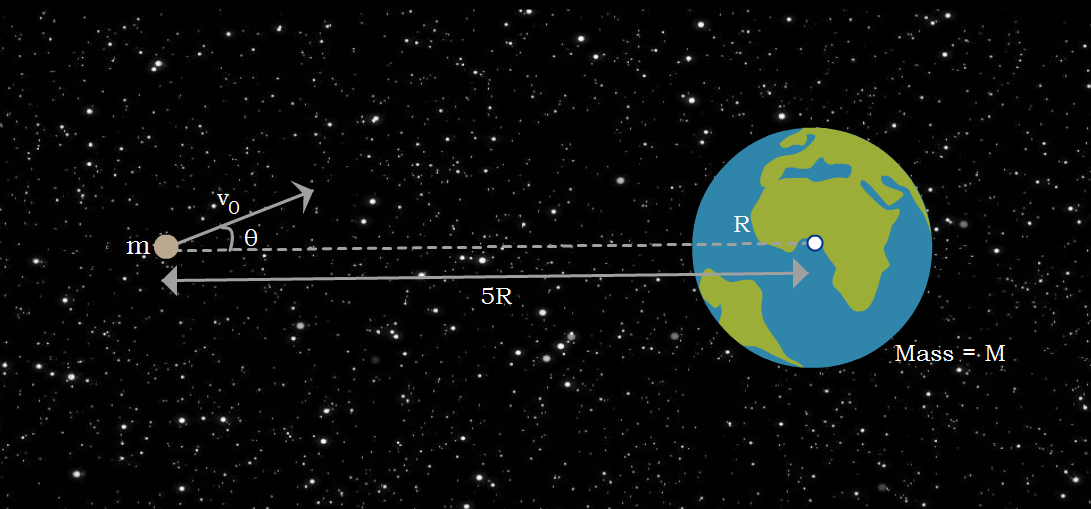
An asteroid of mass $m$ was seen at a distance of $5R$ from the center of Earth with initial velocity $v_0,$ making an angle of $\theta$ with the radial vector from the center of Earth. Due to the mutual gravitational interaction between Earth and the asteroid, the asteroid deviated from its original path, and afterwards it was seen that the asteroid just grazed the surface of Earth and moved on.

If $\theta$ can be expressed as $\theta = \sin^{-1}\left[ \dfrac ab \sqrt{c+ \dfrac{dGM}{eR{v_0}^2}} \right],$ where $a,b,c,d,$ and $e$ are positive integers (not necessarily distinct) and $(a,b)$ and $(d,e)$ are coprime integer pairs.

Evaluate the value of $a+b+c+d+e$ .

Details and assumptions:

Assume there are no other external bodies other than Earth and the asteroid. The only mutual force of gravitation that exists is between them.
Neglect the size of the asteroid, i.e. treat it as a particle of mass $m$ .
$G$ denotes the universal gravitational constant: $G = 6.67 \times 10^{-11} \text{ N m}^2 \text{ kg}^{-2}$ .
$M$ denotes the mass of Earth: $M = 5.972 \times 10^{24} \text{ kg}$ .
$R$ denotes the radius of Earth: $R = 6371 \text{ km}$ .
Assume that rotation and revolutions of Earth are absent for this problem.
Assume that there is no atmosphere near the surface of Earth.
Assume Earth is a uniform sphere with no geographical deformities or man-made structures.

The answer is 20.

1 solution

William G.
Feb 6, 2017

Relevant wiki: Applying Kepler's Laws

Let $V$ be the original velocity and $v$ be velocity at the grazing area. Using the conservation of energy, we can write

$\frac{1}{2}m{V^2} - \frac{{GMm}}{{5R}} = \frac{1}{2}m{v^2} - \frac{{GMm}}{R}.$

This gives, $v = \sqrt {{V^2} + \frac{{8GM}}{{5R}}}$

Now, as the only force acting on the asteroid is the gravitational pull which passes through the center of the Earth. Therefore, its torque about the center of the Earth is zero and the angular moment of the asteroid will remain conserved. Hence, applying the Conservation of angular momentum , we can write

$mV \sin \theta 5R = mvR \Rightarrow v= 5V \sin \theta.$

Plugging this value of $v$ in the above equation yields

$\sin \theta = \frac{{\sqrt {{V^2} + \frac{{8GM}}{{5R}}} }}{{5V}} \,\,\, \Rightarrow \,\,\, \theta = {\sin ^{ - 1}}\left( {\sqrt {1 + \frac{{8GM}}{{5R{V^2}}}} } \right).$

Comparing with the form for $\theta$ given in the question we get, $a=1,\, b=5,\, c=1,\, d=8$ , and $e=5$ which gives an answer of $\boxed{20}$ .

Nice solution! You presented it very well without the use of $LaTeX$ .

Tapas Mazumdar - 4 years, 4 months ago

thanks. I have no understanding of latex at all

William G. - 4 years, 4 months ago

.........I don't even know latex how did this happen

William G. - 4 years, 3 months ago

Some moderator or staff member must've done this.

@Brilliant Mathematics Please make the necessary corrections in the solution.

Tapas Mazumdar - 4 years, 3 months ago

@Tapas Mazumdar Assuming you did this, you forgot the coefficient of 1/5 in the arcsin area

William G. - 4 years, 3 months ago

That was another close call!

The answer is 20.

1 solution

0 pending reports