A classical minimization problem
An isosceles trapezoid has its four vertices as follows: . We want to circumscribe an ellipse around the trapezoid. There is an infinite number of such ellipses. We want to choose the one with minimum area. Find that minimum area and report the value of .
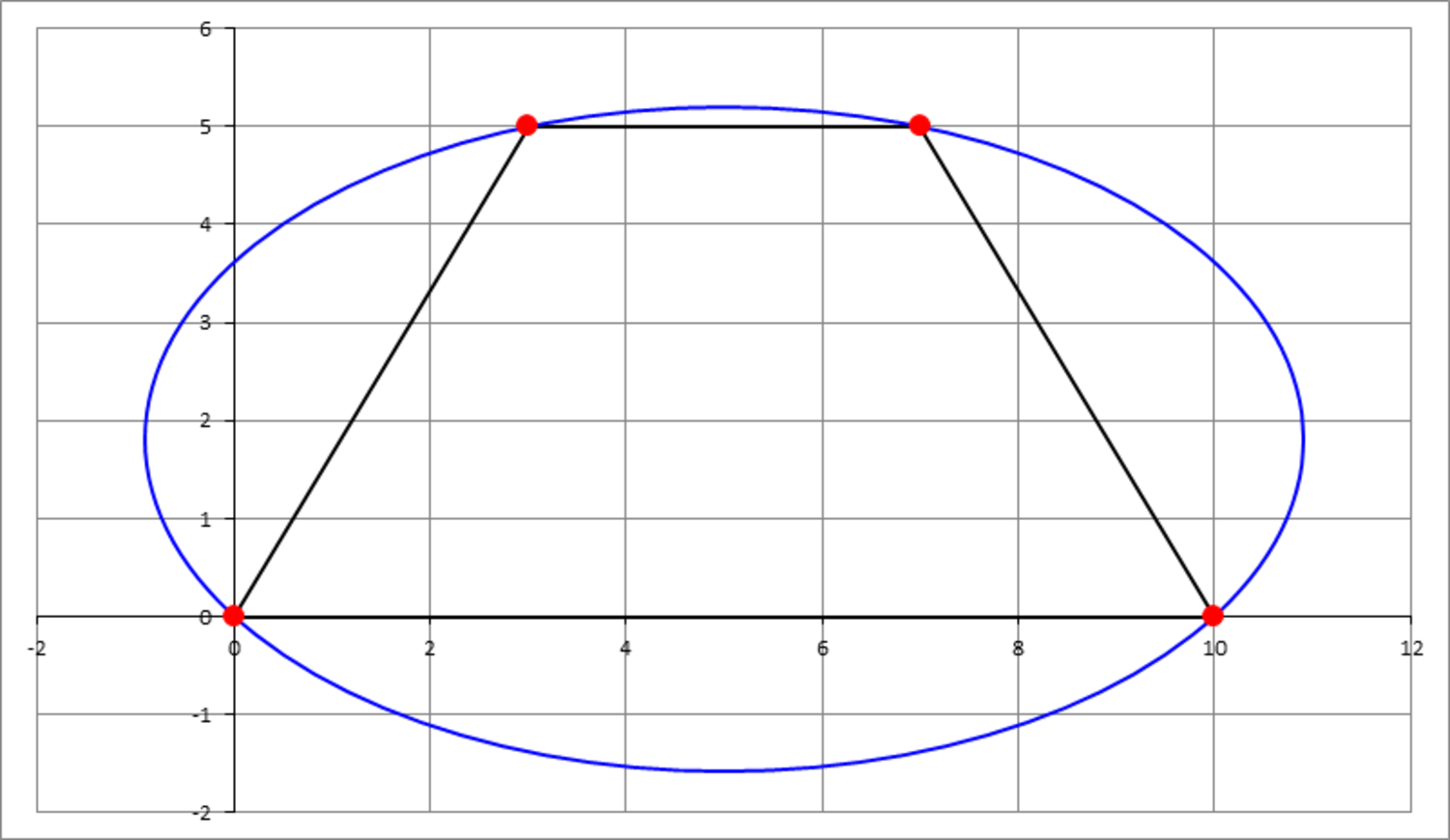
The answer is 6297.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If we translate the trapezoid over ( − 5 , 0 ) , the y-axis bexomes the vertical axis of symmetry. Let y = y 0 be the horizontal axis of symmetry, then we have the following equation for the ellipse: a 2 x 2 + b 2 ( y − y 0 ) 2 = 1 Filling in the coordinates of the two known points ( x , y ) = ( 5 , 0 ) and ( x , y ) = ( 2 , 5 ) gives two equations that must hold: a 2 2 5 + b 2 y 0 2 = 1 ( I ) a 2 4 + b 2 ( 5 − y 0 ) 2 = 1 ( I I )
Subtract 4 b 2 times (I) from 2 5 b 2 times (II) and rearrange to get b 2 = y 0 2 − 2 1 2 5 0 y 0 + 2 1 6 2 5
and rewrite (I) as a 2 = b 2 − y 0 2 2 5 b 2 = 2 5 6 2 5 − 2 5 0 y 0 2 1 y 0 2 − 2 5 0 y 0 + 6 2 5
Now since the quantity a 2 b 2 is a constant times the area squared ( A = π a b ), at minimum area it must be stationary. a 2 b 2 = 2 1 ( 2 5 − 1 0 y 0 ) ( 2 1 y 0 2 − 2 5 0 y 0 + 6 2 5 ) 2 Using the quotient and chain rules we set the derivative to 0:
d y 0 d 2 1 a 2 b 2 = ( 2 5 − 1 0 y 0 ) 2 2 ( . . . ) ( 4 2 y 0 − 2 5 0 ) ( 2 5 − 1 0 y 0 ) + 1 0 ( . . . ) 2 = 0
where (...) is shorthand for 2 1 y 0 2 − 2 5 0 y 0 + 6 2 5 . Because we demand that b = 0 we can divide by (...) and simplify to find
6 3 y 0 2 − 4 6 0 y 0 + 6 2 5 = 0 This gives two values for y 0 . The larger value would give b 2 < 0 , so we take the smaller root y 0 = 1 2 6 4 6 0 − 4 6 0 2 − 4 × 6 3 × 6 2 5 = 1 . 8 0 4 8 0 8 9 9 . . . From y 0 we calculate A = π a 2 b 2 = 6 2 . 9 7 4 6 1 3 . . . and find the answer ⌊ 1 0 0 A ⌋ = 6 2 9 7