A clever manipulation
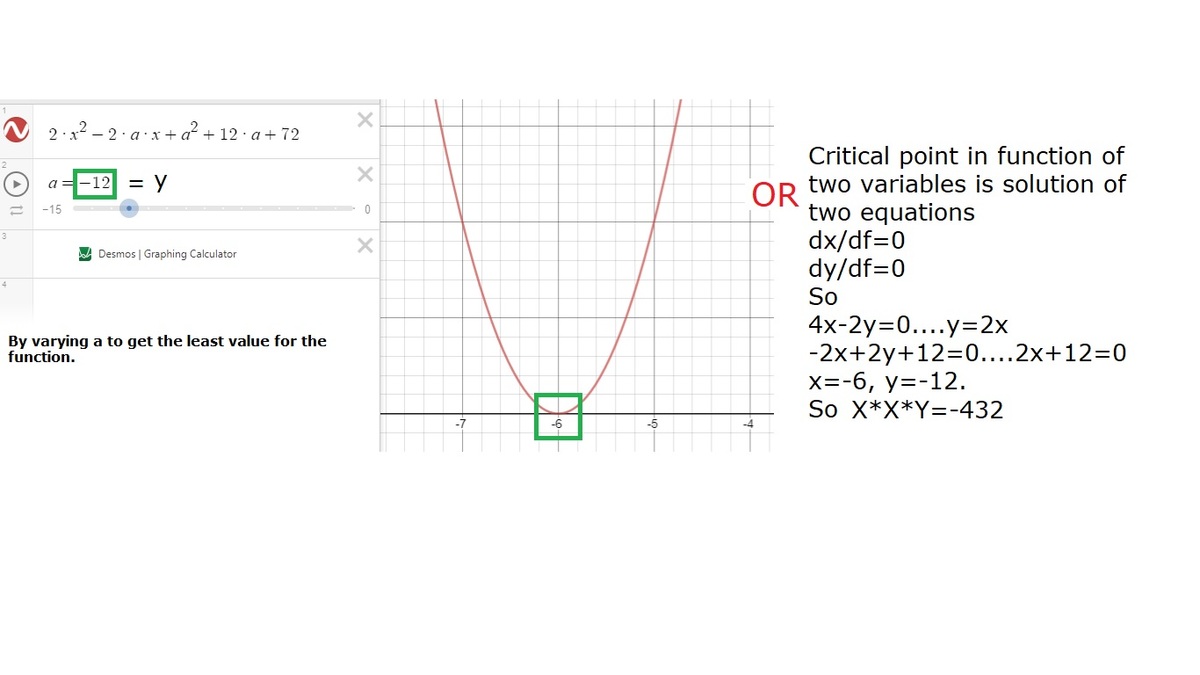
Suppose x and y are real numbers such that 2 x 2 + y 2 − 2 x y + 1 2 y + 7 2 ≤ 0 . Find the value of x 2 y .
The answer is -432.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Multiply the equation by 2:
⟹ 4 x 2 + 2 y 2 − 4 x y + 2 4 y + 1 4 4 ≤ 0
⟹ ( 4 x 2 + y 2 − 4 x y ) + ( y 2 + 2 4 y + 1 4 4 ) ≤ 0
⟹ ( 2 x − y ) 2 + ( y + 1 2 ) 2 ≤ 0
Since the sum of squares are always non-negative, we must have 2 x − y = 0 and y − 1 2 = 0 . Hence x = − 6 and y = − 1 2 .
This gives us x 2 y = ( − 6 ) 2 ⋅ ( − 1 2 ) = − 4 3 2 .
say x = p and y = p + q . We have:
2 p 2 + ( p + q ) 2 − 2 p ( p + q ) + 1 2 ( p + q ) + 7 2 ≤ 0
p 2 + q 2 + 1 2 p + 1 2 q + 7 2 ≤ 0
p 2 + 1 2 p + 3 6 + q 2 + 1 2 q + 3 6 ≤ 0
( p + 6 ) 2 + ( q + 6 ) 2 ≤ 0
Now, we can see p = − 6 and q = − 6 . Which gives x = − 6 and y = − 1 2
Finally, x 2 y = − 1 2 ⋅ 3 6 = − 4 3 2
2 x 2 + y 2 − 2 x y + 1 2 y + 7 2 2 x 2 − 2 x y + ( y + 6 ) 2 + 3 6 x 2 + x 2 − 2 x ( y + 6 ) + 1 2 x + ( y + 6 ) 2 + 3 6 ( x + 6 ) 2 + ( x − ( y + 6 ) ) 2 ≤ 0 ≤ 0 ≤ 0 ≤ 0
We note that the LHS ≥ 0 . Hence there is only one solution that is the LHS = ( x + 6 ) 2 + ( x − ( y + 6 ) ) = 0 , which is only true when x + 6 = 0 and x − ( y + 6 ) = 0 . Therefore, x = − 6 , y = − 1 2 , and x 2 y = − 4 3 2 .