A coffee break geometry problem 2

Geometry Level 3

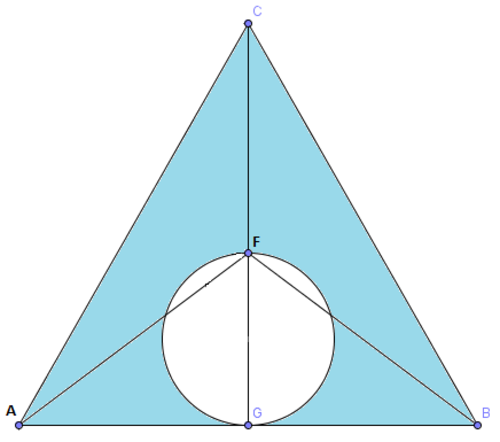This time the tables are turned, instead of triangles cut out of a circle, there is a circle cut out of a isosceles triangle! Again you must find the area of the shaded region.

You are given that the angle formed by FCB is 29.74 degrees, the angle CBF is 23.39 degrees, and the angle CGB is 90 degrees. The length of CB is 8.06

The length of the line segments AB, CF, FG, and FB are each whole numbers.

*Edit added for clarification: AF is a whole number, and CFG is a straight line.

The answer is 20.93.

2 solutions

Chew-Seong Cheong
Sep 16, 2014

Let $CB = l = 8.06$ and $\angle FCB = \theta = 29.74^o$ , therefore,

$CG = h = l \cos{\theta} = 8.06\cos {29.74^o} = 7$

$GB = a = l \sin{\theta} = 8.06\sin {29.74^o} = 4$

$\angle FBG = \phi = \angle CBG - \angle CBF$

$\quad \quad \quad = (90 - \angle FCB) - \angle CBF = 90 - 29.74 - 23.39 = 38.67^o$

$FG = b = a \tan{\phi} = 4 \tan{38.67^o} = 3$

The area of the $\triangle ABC = A_\triangle = \frac{1}{2}(2a)h = ah = 4\times 7 = 28$

The area of circle $FG = \pi r^2 = pi \times (\frac{3}{2})^2 = 7.0686$

Therefore , the area of shaded region $= 28 - 7.0686 = \boxed{20.93}$

The question didn't tell me that this triangle is an isosceles triangle.

Adam Zaim - 6 years, 8 months ago

No, but the diagram show it and the answer works out. It is only a 10 point question. It cannot be that tough.

Chew-Seong Cheong - 6 years, 8 months ago

Jake Maason
Sep 15, 2014

We can determine the angle CFB as equal to (180-29.74-23.39) or (126.87). With this new information we can apply the law of sines to determine CF and FB. There are several ways to solve this problem, the following is just one.

$\text{Step 1:} \\ \frac{8.06}{sin(126.87)} = \frac{FB}{sin(29.74)} \\ \rightarrow FB = \frac{(sin(29.74)*8.06)}{(sin(126.87)} \\ \text{FB is approximately equal to 4.99786... } \\ \text{Since we know FB is a whole number, we are justified in} \\ \text{rounding up from this approximation. Thus FB = 5}$

$\text{Step 2:} \\ \text{To find GB we can again apply the law of sines} \\ \frac{CB}{sin(CGB\measuredangle)} = \frac{GB}{sin(GCB\measuredangle)} \\ \rightarrow \frac{8.06}{sin(90)} = \frac{GB}{sin(29.74)} \\ \rightarrow GB = \frac{sin(29.74)*8.06}{sin(90)} \\ \text{We get GB = 3.99828... we are again justified in rounding up. Thus GB = 4}$

$\text{Step 3:} \\ \text{We can now determine FG using the Pythagorean theorem} \\ FG^2 =FB^2 - GB^2 \\ \rightarrow FG = \sqrt{5^2 - 4^2} = 3 \\ \text{Thus the radius of the circle is} \frac{3}{2}$

$\text{Step 4:} \\ \text{We can also use the Pythagorean theorem in the same way} \\ \text{to solve the length of CG since we know CB = 8.06 and GB = 4.} \\ \text{We find the result to be CG = 7 (since we know CG is a whole number)}$

$\text{Step 5:} \\ \text{Finally we subtract the area of the circle from the area of the Triangle} \\ \text{The base of the triangle is 2GB, and the height is 7.} \\ \text{Thus we find the area of the shaded region to be} \\ (\frac{1}{2}*8*7) - ((\frac{3}{2})^2 * \pi) \\ = 20.93$

This is the way I got the answer, but I had to make a few assumptions along the way. The first (really picky one) was that $CFG$ was indeed a straight line; I realize that you have given us that $\angle CGB = 90$ degrees, but that doesn't necessarily mean that lines $CG$ and $CFG$ are one and the same. They do appear to be drawn that way, but an assumption had to be made in any event.

The more substantive assumption that had to be made was that segment $AG$ has the same length as segment $GB$ . This can only be implied if $AF$ is also a whole number, in which case, since $FG = 3$ and $\angle AGF = 90$ degrees, we must have $AG = 4$ and $AF = 5$ . If it is not given that $AF$ is also a whole number, then even though it is given that $AB$ is a whole number, and hence $AG$ is a whole number, we could have $AG$ being any whole number.

So this is a good problem, but I think that you will need to add that either the triangle $ACB$ is isosceles or that segment $AF$ is also a whole number, (the latter would be preferable). You might also want to include a mention that $CFG$ is a straight line to be ultra-precise. Thanks in advance for considering my suggestions. :)

Brian Charlesworth - 6 years, 8 months ago

Yes very good point, I edited it for clarification using your suggestions. Thanks!

Jake Maason - 6 years, 8 months ago

A coffee break geometry problem 2

The answer is 20.93.

2 solutions

0 pending reports