A coffee break geometry problem #3
Four circles have a radius of 3 and are arranged perfectly side by side into a 2x2 grid. What is the area of the shaded region in the center?
The answer is 7.73.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
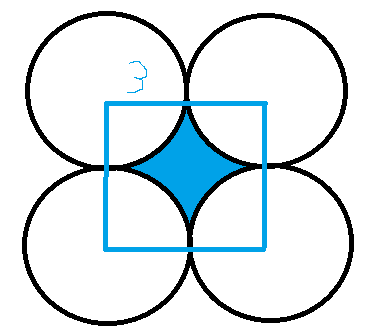In the picture,a square is made by joining the centers of the circles.The side is twice the radius,meaning that it is
2
(
3
)
=
6
units long.So area of square=
l
2
=
6
2
=
3
6
.The four quarter circles make one full circle.Which has area
π
r
2
=
π
(
3
)
2
=
9
π
.So shaded area=
A
r
e
a
o
f
s
q
u
a
r
e
−
A
r
e
a
o
f
c
i
r
c
l
e
=
3
6
−
9
π
≈
7
.
7
3
First we observe that since they are arranged perfectly in a 2x2 grid, a square can be constructed by connecting the centers of each circle with 4 lines segments.
Inside the square that we have just constructed, we see that there are 4 quarter circles. Each of these quarter circles will have 1/4 the area of the circle that they are cut off from.
So now we simply subtract the area of these 4 quarter circles from the area of the square we have constructed. The area that remains is that of the shaded region. We know that the length of each line segment is 6 because they are equal to 2r. Thus:
6 2 − 4 ∗ ( 4 1 ∗ 3 2 ∗ π ) ≈ 7 . 7 3