A coffee break geometry problem #4
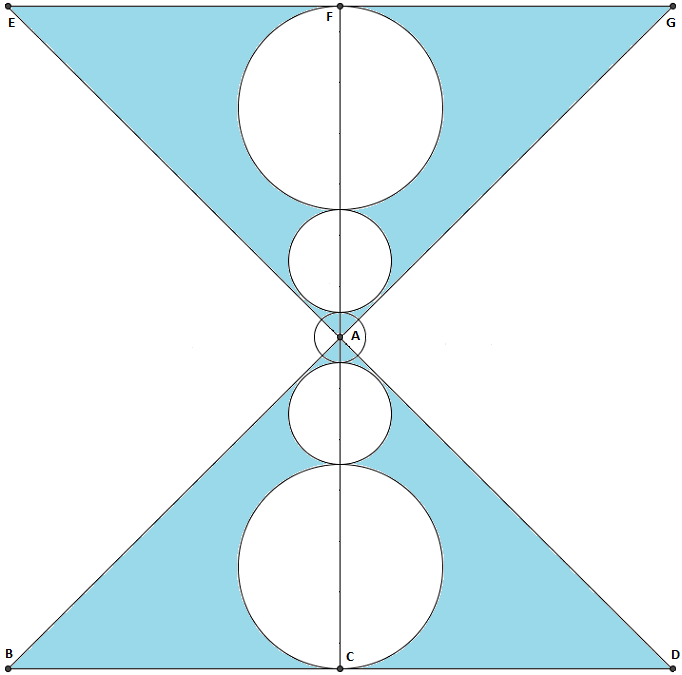 The radius of the smallest circle is equal to
The radius of the smallest circle is equal to
The circles with a medium size each have a radius 2 times that of the smallest circle. The largest circles each have a radius 4 times that of the smallest circle.
BG is perpendicular to ED. The line segment AC bisects ABD into equal parts.
Find the area of the shaded regions.
Extra information:
- BC = CD = EF = GF
- EA = AD
- BA = AG
- ED = BG
- Point 'A' is the center of the smallest circle.
- All line segments between the points are straight lines.
The answer is 212.336.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First, we have that
lim x → 1 x 2 − 1 3 x 2 − 5 x + 2 = lim x → 1 ( x + 1 ) ( x − 1 ) ( 3 x − 2 ) ( x − 1 ) = lim x → 1 x + 1 3 x − 2 = 2 1 ,
and lim x → 5 x 2 − 2 5 2 0 x − 1 0 0 = lim x → 5 ( x + 5 ) ( x − 5 ) 2 0 ( x − 5 ) = lim x → 5 x + 5 2 0 = 2 .
Thus the radius of the smallest circle is ( 2 1 ) ∗ 2 = 1 , and so the radii of the medium size and largest circles are 2 and 4 , respectively.
Looking at just the lower triangle, its height h will be the sum of the radius of the smallest circle plus the diameters of the two other circles, i.e., h = 1 + 2 ∗ 2 + 2 ∗ 4 = 1 3 . Now given the inherent symmetries of the diagram, and since B G ⊥ E D , we know that both triangles are isosceles right triangles with height 1 3 and base length 2 ∗ 1 3 = 2 6 , and thus each has an area of ( 2 1 ) ∗ 2 6 ∗ 1 3 = 1 6 9 .
Now to find the area of the shaded region, we need to subtract the areas of two each of the medium and largest circles from the combined area of the two triangles. This results in an area value of
2 ∗ 1 6 9 − 2 ∗ π ( 2 2 + 4 2 ) = 3 3 8 − 4 0 π = 2 1 2 . 3 3 6
to 3 decimal places.