A coffee break geometry problem
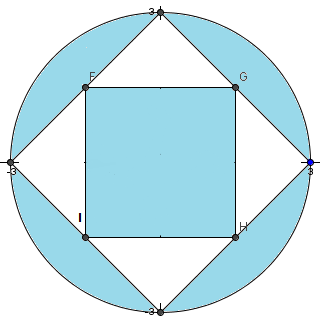 Here is a circle with a radius of 3.
Here is a circle with a radius of 3.
It has 4 triangles cut out of it.
What is the remaining area of the shaded in region?
The answer is 19.27.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
14 solutions
I didn't even see the big square .... Strategic thinking , thumbs up .
(1) Area of Circle = 9π (2) Side of big square =3√2, so area of big square will be =18 (3) Side of small square will be (3√2/2)* √2 =3 , therefore area of small Square will be = 9 (4) Area of shaded region will be = 9π-18+9 = 9(π-1) =19.27
Actually, given the length of a side of the larger square, we can formulate it's area to be 18, and so we now have 9pi-18. Then, we add the area of the smaller square, with a diagonal of 3sqrt{2}, a length of 3, and area of 9. 9pi-18+9=9pi-9.
19.26 sq unit
I got value of 9 pi - 9 wrong.
so interesting
how side of small square comes 3 ?????
GOT IT :D 19.27! :D
easy ....but did some mess :( ......calculated .5 1.5^2 instead of .5 1.5*3 while calculating area pf the triangle
The area of the shaded region is
(area of circle) - (area of larger square) + (area of smaller square).
The area of the circle is π ∗ r 2 = 9 π .
For the larger square, note first that the centers of the circle and square coincide. Now draw a triangle with two vertices being adjacent corners of the square and the center of the circle as the third vertex. This is a right triangle with short sides both length r = 3 , so the hypotenuse has length 3 2 . Since the hypotenuse is the also side of the larger square, the larger square has an area of ( 3 2 ) 2 = 1 8 .
For the smaller square, look first at the upper triangle in the diagram. It is a right triangle with short sides length 2 3 2 , (since its lower two vertices correspond with the midpoints of the sides of the larger square), and thus has a hypotenuse of length 2 3 2 2 = 3 . Since the hypotenuse is also the side of the smaller square, the smaller square has an area of 3 2 = 9 .
Thus the area of the shaded region is 9 π − 1 8 + 9 = 9 ( π − 1 ) = 1 9 . 2 7 to two decimal places.
Alternately, we could first note that the 4 triangles have a combined area that is the same as the smaller square. Then the area of the shaded region is just the area of the circle minus the area of the smaller square. As found above, the area of the smaller square is 9 , so the area of the shaded region is 9 π − 9 as found before.
nice solution
nice question, could not find correct solution
The white area and the smaller square are just equivalent, (just imagine that you fold all the white triangles to the inside, and they perfectly fit. Then the shaded area = the circle - the smaller square:
where A= shaded area B = circle area and C = small square then
A= (πrr)-rr A=28.27-9=19.27
This is a fun problem, but it should be noted that the question is unsolvable as worded (without answering it as a function) unless you make the assumption that each cut out is an isosceles triangle containing a 90 degree angle, or that each of the points {F,G,H,I} of the shaded square lie on a straight line. Otherwise triangles whose largest angle is smaller than 90 degrees would yield different answers for the remaining area, and we would not be able to make the nice connection that the diameter of the circle is equal to the side length of the square.
The side of a square within a square within a circle is half the diameter of the circle or = to the radius = 3, the external triangles created by a square within a square are equal to the inner square, therefore the space taken by the 4 triangles being equal to that of the inner square is 3*3 = 9, area of a circle we all know pi radius squared = 28.274333882308139146163790449516, therefore answer = this minus 9 = 19.274333882308139146163790449516, wasn't sure if the solution would accept significant deciaml to 19.2743 but would propose this as a solution
U increase ur intellectual power...
Area of circle = pi * r^2 = 9pi (trivial) Area of larger square = l * w = (6/sqrt(2))^2 = 36/2 = 18* Area of smaller square = l * w = 3 * 3 = 9**
Total shaded = circle - (larger square - smaller square) = circle - larger square + smaller square = 9pi - 18 + 9 = 9pi - 9. (insert halmos symbol here)
- l and w are both 6/sqrt(2) based on the 45/45/90 triangle pattern of x/x/xsqrt(2). If you don't know this one, you can also use l = w for a square to just get w^2 + w^2 = 6^2 using pythagorean theorem, since the square's diagonal is also the diameter of the circle (6).
** This square's length and width are both 3 because that's what you get from the pythagorean theorem if you plug in half the l and w of the larger square, i.e. 3/sqrt(2), as a and b. Alternately, you can use the identity that says a square connecting the midpoints of a larger square has half of the larger square's area.
Area of the shaded region=(area of the circle)-(area of big square)+(area of small square),Now note that diagonal of the big square=diameter of the circle,so side of the big square=6/(sqrt2),then area of it={6/(sqrt2)}^2=18,now note closely the diagonal of the small square=side of the big square,we know that diagonal of a square=(sqrt2) * a,so (sqrt2) * a={6/(sqrt2)} or a={6/(sqrt2 * sqrt2)}=6/2=3,so area of the small square=3^2=9,and the area of the circle=pi * 3^2=9pi,hence area of the shaded region=9pi-18+9=19.2744
I DID IT SO THAT MY SOLUTION CAME AS:
9+9pi-(2*-/4.5)^2
which I got 19.2743338823081...and I got so many decimal places because I know pi to 63 decimals! but I only used 2 decimals
in addition to that, this is how I got the -/4.5 part a^2+b^2=9... I knew they were right angles a^2+a^2=9... because a=b (-/4.5)^2+(-/4.5)^2=9
that was how I got the -/4.5 part!
the square was x^2 and x=2*-/4.5
ALSO: just if you didn't notice... -/ means square root
S c=28.26, St(fg3)=2.24 , S des t=8.96 et S=19.30
From given radius we find area of circle Pi r^2 =28.26 sq.cm We thenfind areas of bigger and small squares in side circle by diagonal length of bigger square =6 cm and areas as 18 and 9 sq.cm Subtracting from 28.28 value 18 we get area 19.26 Ans K.K.GARG,india
but the answer is 19.27...
Mid point of iH is o and 2▲IOH=▲IH3 required area = area of circle - 8area of ▲IOH = 9×3.14-9 = 19.27
(1) Area of Circle = 9π (2) Side of big square =3√2, so area of big square will be =18 (3) Side of small square will be (3√2/2)* √2 =3 , therefore area of small Square will be = 9 (4) Area of shaded region will be = 9π-18+9 = 9(π-1) =19.27
The square consists of 4 of the white triangles . So, the square side length is 3 and triangle base length is double the height which means that it's equal to 3 . Area of circle - 4(area of triangle) is the solution .
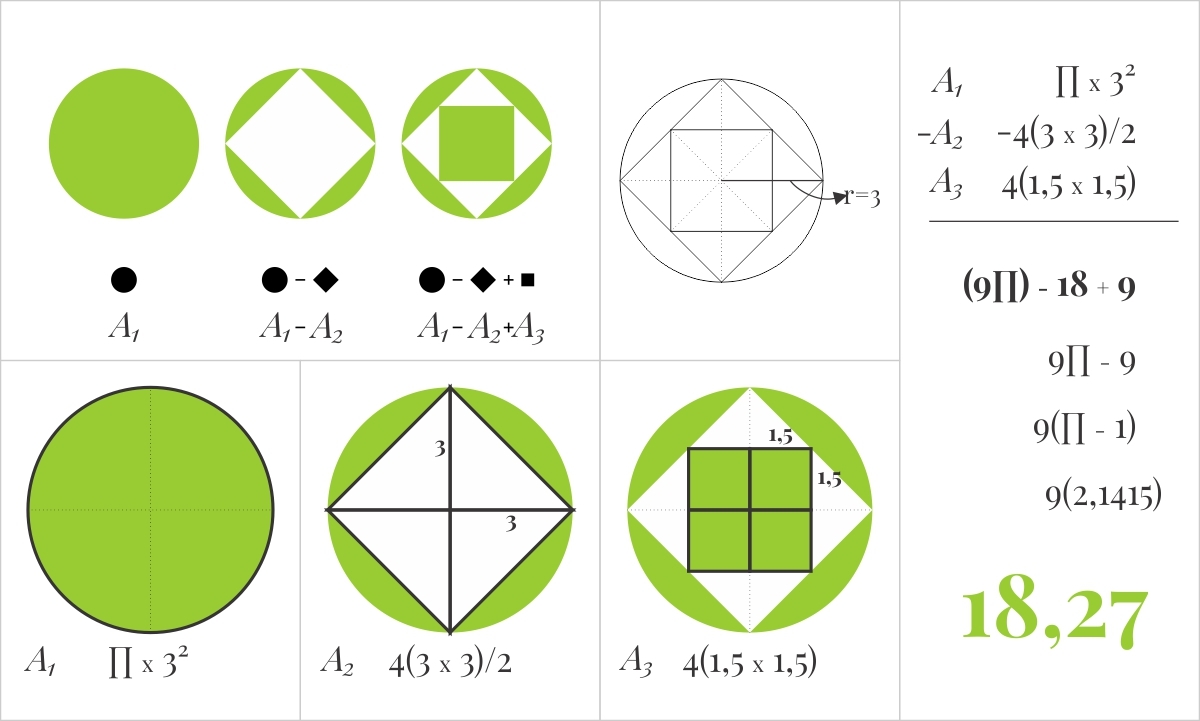
The area of the big square (the one that touches the circle) is 2 1 d i a m e t e r 2 = 2 1 ∗ 6 ∗ 6 = 1 8 since we can see it as a rhombus. The 4 triangles then altogether are half of the square, so their area is 9 . The area of the shaded region is the area of the circle minus the area of the triangles which is 9 π − 9