A Coin Flipping Game

Let $P_{1}$ be the probability that you win and $P_{2}$ be the probability that your friend wins. If you toss tails, (probability $1/2$ ), then if we imagine that the game was "reset" then your friend would win this "reset" game with probability $P_{1}$ . This implies that $P_{2} = \dfrac{1}{2} \times P_{1}$ .

Now as one of you will win eventually we have that $P_{1} + P_{2} = 1 \Longrightarrow P_{2} = 1 - P_{1} \Longrightarrow \dfrac{1}{2} \times P_{1} = 1 - P_{1} \Longrightarrow P_{1} = \dfrac{2}{3} \Longrightarrow a + b = 2 + 3 = \boxed{5}$ .

The following probability tree can be constructed:

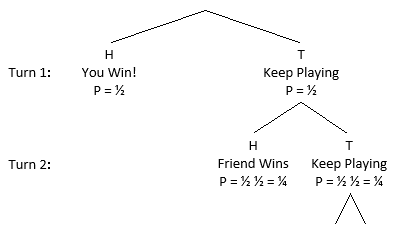
On the first coin flip, there is a $\frac{1}{2}$ probability that you will flip heads and win, but a $\frac{1}{2}$ probability that you will flip tails and the game will continue. If the game continues to a second coin flip, your friend has $\frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4}$ overall probability that he will flip heads and win, but a $\frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4}$ overall probability that he will flip tails and the game will continue. If the game continues back to your turn, the probabilities are the same as your first coin flip but at a $\frac{1}{4}$ ratio. Since the game could potentially continue on forever in this manner, the probability of you winning can be expressed as an infinite sum:

$P = \frac{1}{2} + \frac{1}{4}(\frac{1}{2} + \frac{1}{4}(\frac{1}{2} + \frac{1}{4}(...$

Substituting $P$ into the above equation gives:

$P = \frac{1}{2} + \frac{1}{4}P$

and solving this equation for $P$ gives $P = \frac{2}{3}$ , and $2 + 3 = \boxed{5}$ .