Counting Brackets
Suppose we have competitors in a single-elimination tournament bracket. While they may be seeded in any conceivable permutation, suppose further that there is a fixed, hidden, strict order of skill amongst the players, such that the winner of any single match is deterministic, and the property is transitive: If can beat , and can beat , then can beat .
The number of distinct ways such a tournament can be seeded is, trivially, , but what about the number of distinct ways such a tournament can play out? For example, a 2-person tournament can only ever finish one way: With the best player finishing first, and the other second. A four-person tournament is more interesting. The best player will always finish first, but depending on the seeding, it might be the case that the second-best player finishes second, or the third-best player finishes second, with the remaining players taking an equivalent "3rd/4th" place in the final standings.
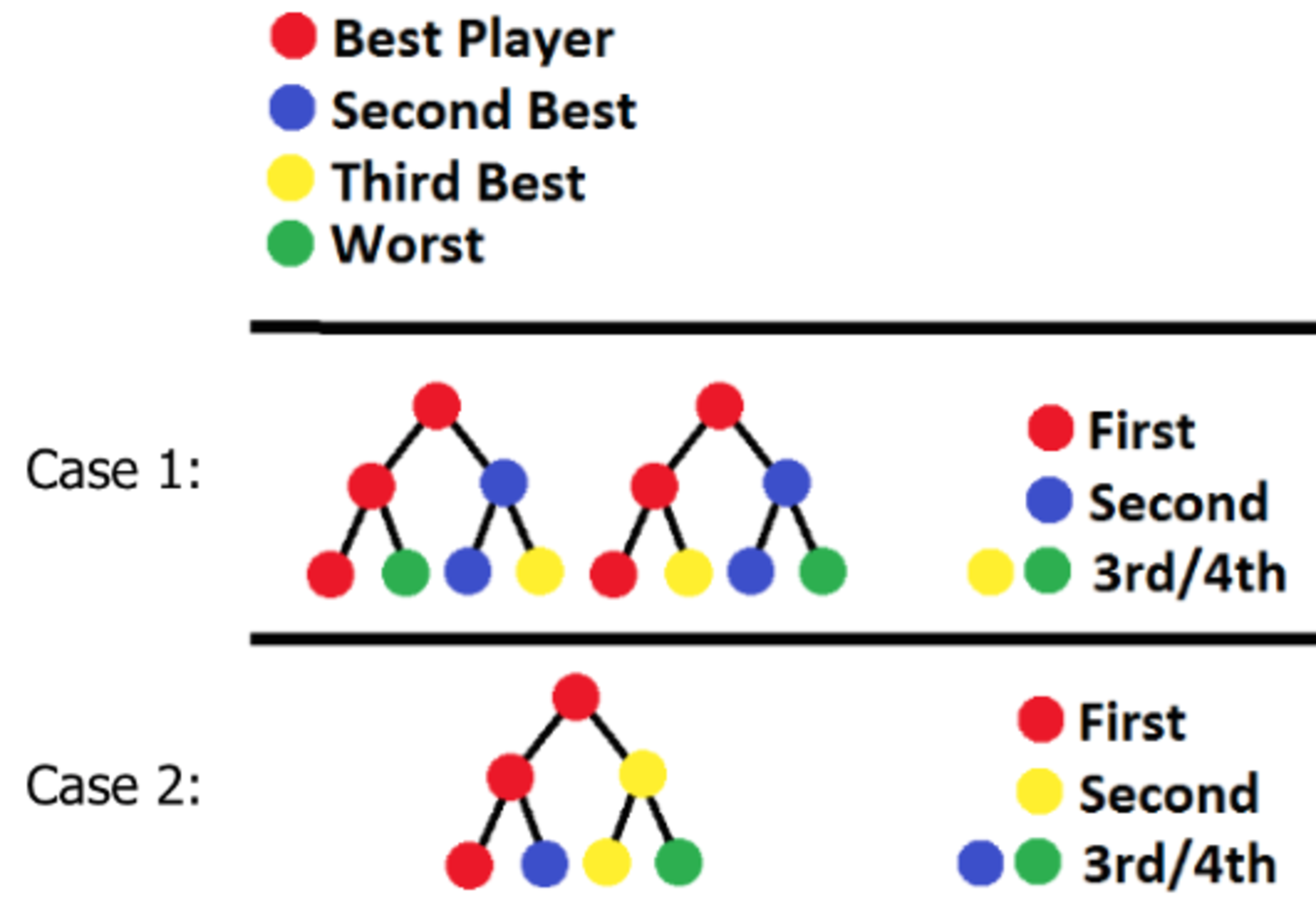
Thus, there are precisely 2 ways a 4-person tournament might conclude. More precisely speaking, two tournaments are said to conclude differently if and only if there exists at least one player who got a different placement between the two outcomes. Places in a tournament are, uniquely and distinctly, '1st', '2nd', '3rd-4th', '5th-8th', '9th-16th', etc. etc.
There are 28 ways that an 8-person tournament might conclude, depending on seeding.
How many ways can a 64-person tournament conclude?
The answer is 78620747792837680789505546400.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Combinations - Problem Solving
The nature of a tournament bracket easily lends itself to recursive algorithms and formulas to compute things about them. In this case, however, there is a much simpler solution, requiring a little combinatorics and a little math on top.
The answer is clearly very, very big, so we need a way to abstract the problem. We need to determine the number of distinct ways there are to categorize the 2 n competitors into n + 1 buckets, each the size of an incremental power of 2 , but with the added restriction that it must be possible for such an outcome to occur given the hidden skill order! This is what makes the problem tricky.
For simplicity, let's number the players in skill order, so that player 1 beats everyone, player 2 beats everyone except player 1 , and player 2 n loses to everyone. Now, suppose we already know the number of ways a tournament of 2 n − 1 players can play out: How many ways can one of 2 n players play out?
After the first round, we have 2 n − 1 players, which comprise some subset of the original set, and therefore has its own order. Furthermore, the number of ways the rest of the rounds can play out is independent of how the first round played out: Therefore, we need only determine the number of possible sets of 2 n − 1 losers that may occur after the first round, multiplying this by our answer for the smaller tournament bracket yields the answer we want.
Intuitively, one might say that there are ( k 2 k ) ways to choose the losers from 2 k players, but this is incorrect - player 1 could be designated a loser by that logic, and that is impossible! So how many ways are there to pick losers?
Suppose we assign each player a color: Red if they're a winner, blue if they're a loser, and then we list the players in skill order, starting with the best. Clearly, the first color must be red, and then the next one can be blue or red, but if it is blue, the third color again must be red. More succinctly, in order for pairings to be determined such that each player's color is fulfilled, it must be the case that, at any index in the list, the number of reds preceding the index is greater than or equal to the number of blues preceding the index. It is also sufficient for a list to be qualifying if this property holds, since one can produce a valid set of pairings by simply iterating directly through the list, collecting winners as they are come across, and doling them out arbitrarily for each loser iterated over.
The number of such lists is equivalent to the number of Dyck words of length 2 n , or the number of random walks of length 2 n starting at zero, and ending at zero, with equally probable steps of + 1 and − 1 , without ever going negative. All of these things are given by the Catalan Numbers .
Therefore, we can define f ( n ) as the number of ways a tournament of 2 n players can finish, as:
f ( 1 ) = 1
f ( n > 1 ) = C 2 n − 1 ⋅ f ( n − 1 )
f ( n ) = Π k = 1 n − 1 C 2 k
Where { C n } are the Catalan Numbers, computed as C n = n + 1 1 ( n 2 n ) .
And f ( 6 ) = C 3 2 C 1 6 C 8 C 4 C 2 = 7 8 6 2 0 7 4 7 7 9 2 8 3 7 6 8 0 7 8 9 5 0 5 5 4 6 4 0 0 .