A probability problem by Darel Gunawan
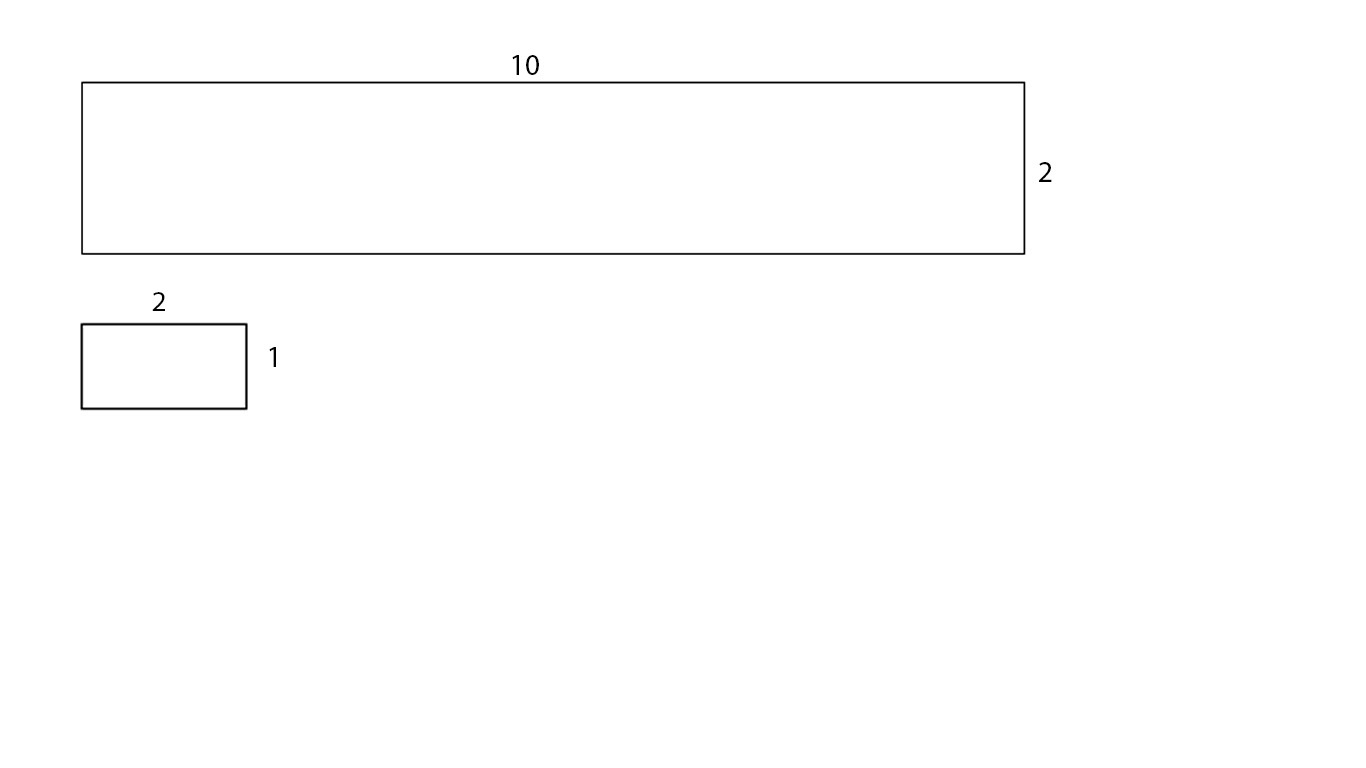
A
rectangle is about to be covered with
rectangles.
In how many ways can this be done?
The answer is 89.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let f ( n ) be the number of ways to cover a n × 2 rectangle, for n ≥ 1 , with 1 × 2 rectangles. Clearly, f ( 1 ) = 1 and f ( 2 ) = 2 .
Now, consider a n × 2 rectangle, for n ≥ 3 . Firstly, draw an 1 × 2 on an end, as follows:
Consider the ( n − 1 ) × 2 rectangle of the right side; the number of ways to cover it is given by f ( n − 1 ) .
Secondly, draw an 2 × 1 rectangle on an end, as follows:
The space below (or above) only can be covered by another 2 × 1 . Consider the ( n − 2 ) × 2 rectangle of the right side; the number of ways to cover it is given by f ( n − 2 ) .
If you place a 2 × 1 rectangle on another position of the n × 2 , the left end of the n × 2 rectangle can be covered in one of the two ways that we have studied, so another possible configuration will have been included in f ( n − 2 ) or f ( n − 1 ) , therefore, the number of ways to cover a n × 2 rectangle is recursively given by the following expression:
f ( n ) = f ( n − 1 ) + f ( n − 2 )
We see that this is how Fibonacci sequence is defined (but f ( n ) would be f n + 1 ). Hence, we are looking for f ( 1 0 ) , which is f 1 1 = 8 9 .