Rough figure
Probability
Level
4
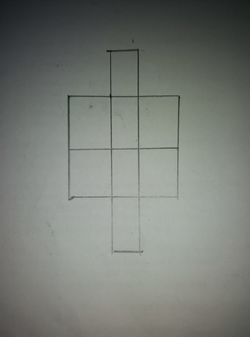 Six P's have to be placed in the squares of the diagram given above such that each column contains at least one P.In how many ways can this be done?
Six P's have to be placed in the squares of the diagram given above such that each column contains at least one P.In how many ways can this be done?
The answer is 26.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Whenever there's an atleast in the wording of the question, we can use case cancellation method.
Total number of ways of filling 6 Ps in 8 squares is equal to 2 ! 6 ! 8 ! = 28.
Now notice that if we have to fill 6 Ps in only two columns, there are 2 ways to do that ( the middle column+one of the two side columns are taken).
To fill them in one column would be an impossible case.
Now cancelling 2 from 28, we get 26 as the answer.