Combinations possible??
Probability
Level
4
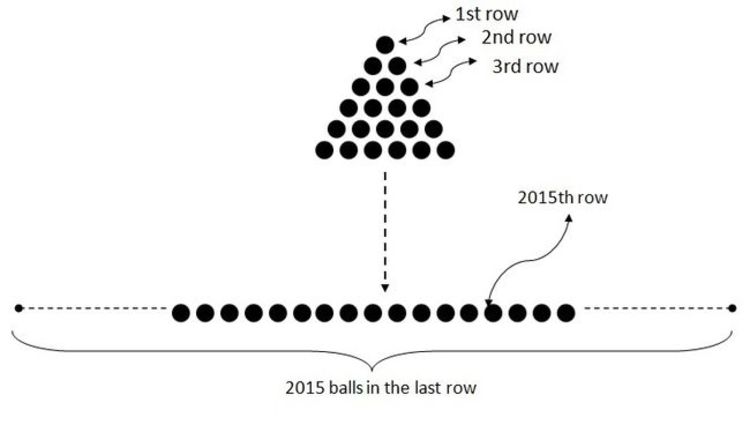 An equilateral triangle is made using balls (As shown). It has got 2015 rows. What are the number of ways you can select two adjacent balls in this equilateral triangle?
An equilateral triangle is made using balls (As shown). It has got 2015 rows. What are the number of ways you can select two adjacent balls in this equilateral triangle?
The answer is 6087315.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The three vertices of the triangle have, by observation, 2 adjacent balls each... thus 2 options each;
3 × 2
the total number of balls on each edge leaving aside the vertices is 2013... each has, by observation, 4 options for adjacent balls.
3 × 2 0 1 3 × 4
Counting the total number of balls in such an equilateral triangle is equivalent to solving the sum of the first 2015 natural numbers... since clearly starting from 1 there is an increase of one ball in each row till 2015. (This is the concept of Triangular Numbers ) ...
The number of balls except for the three edges have to be counted. Each of the balls in this number has, by observation, 6 adjacent balls, i.e. 6 options. So this can solved as
{ 2 2 0 1 5 × 2 0 1 6 − ( 2 0 1 3 × 3 + 3 ) } × 6
Now the Grand Total comes out to be....
[ { 2 2 0 1 5 × 2 0 1 6 − ( 2 0 1 3 × 3 + 3 ) } × 6 ] + ( 3 × 2 0 1 3 × 4 ) + ( 3 × 2 )
Since this is clearly understood that all cases are being counted twice (since adjacent balls are in pair, and counting is performed from both sides), and since the question only asks to make selections, implying the order does not matter... The solution to the question will be...
2 [ { 2 2 0 1 5 × 2 0 1 6 − ( 2 0 1 3 × 3 + 3 ) } × 6 ] + ( 3 × 2 0 1 3 × 4 ) + ( 3 × 2 ) = 6 0 8 7 3 1 5