Count 'em All 14!
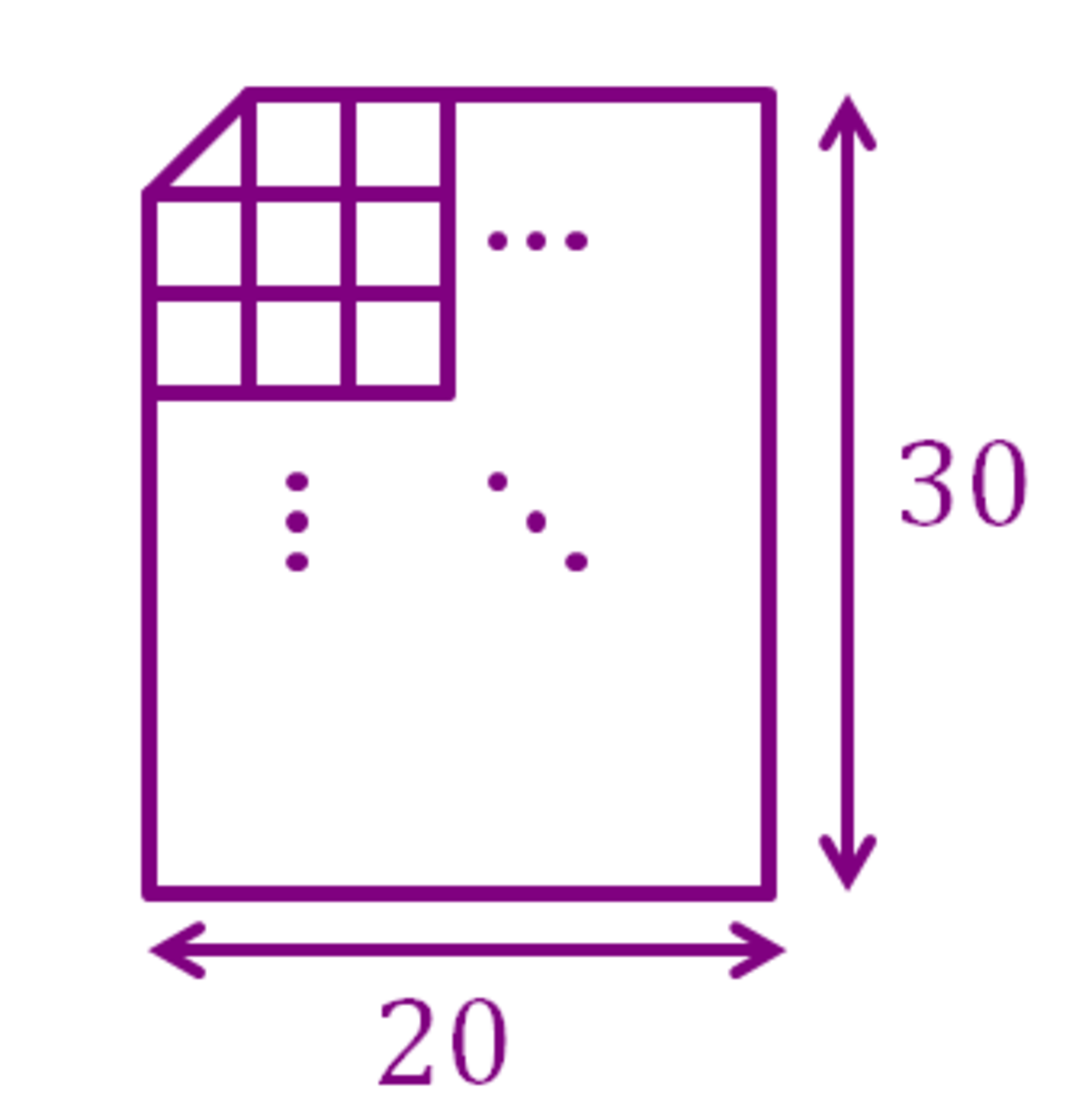
The figure above shows a 2 0 × 3 0 grid but with one of its corners cut off forming a triangle.
Count the total number of quadrilaterals in the grid above.
Clarification :
- A quadrilateral is a polygon that has 4 sides.
This is one part of Quadrilatorics .
The answer is 97098.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I will provide a sketch to show that the number of quadrilaterals in an a × b grid with one of its corners cut off forming a triangle is 4 a b ( a + 1 ) ( b + 1 ) − ( a − 1 ) ( b − 1 ) − 1
You can see the full details of this proof in my solution to Yes, Scissors Are Required (Count em' All 12!) , if you've already seen it, you may safely skip this part. :D
Proof:
Pretend that the corner isn't cut and the grid is perfectly rectangular. The number of quadrilaterals in this perfect a × b grid according to this note is 4 a b ( a + 1 ) ( b + 1 ) .
We now want to remove all quadrilaterals that will turn into pentagons or triangles once the corner is cut.
Note that we can construct a quadrilateral by selecting two squares (possibly the same square) as its opposite corners, if one corner is fixed on the to-be-cut corner square and its opposite corner is not on the same row or column as the to-be-cut corner square, then this quadrilateral will be cut into a pentagon. The number of these soon-to-be pentagons is ( a − 1 ) ( b − 1 ) .
On the other hand, we also want to remove the to-be-cut corner square itself, because it will be cut into a triangle.
Hence the number of quadrilaterals left is 4 a b ( a + 1 ) ( b + 1 ) − ( a − 1 ) ( b − 1 ) − 1 . □
Now, with this formula, substituting a = 2 0 and b = 3 0 , we would get 9 7 0 9 8 .
Thè number of quadrilaterals in ( 2 0 × 3 0 ) grid
= n = 1 ∑ 2 0 × n = 1 ∑ 3 0
= 2 1 0 × 4 6 5
= 9 7 6 5 0
Now, it has one edge cut, so all the quadrilaterals which includes the cut part as one of its edge would not be counted. But, in this process the number of quadrilaterals which have either 1 row or 1 column would not be counted, because they become trapezium which is a quadrilateral.
Careful counting shows that there are [ 1 9 ( 2 9 + 1 9 ) + 1 0 ( 1 9 ) ] = 1 1 0 2 such quadrilaterals which have the cut part as their edge. But we ca express one quadrilateral in two forms. For example, a ( 1 × 4 ) quadrilateral would co-incide with ( 4 × 1 ) quadrilaterals. So, all the 1 1 0 2 quadrilaterals are counted twice in the process, so, the number of quadrilaterals which have to be excluded are 2 1 1 0 2 = 5 5 1
But, now we see that the cut edge forms a triangle, so that too have to be excluded.
So, the total number of quadrilaterals are [ ( 9 7 6 5 0 − 5 5 1 ) − 1 ]
= [ 9 7 0 9 9 − 1 ]
= 9 7 0 9 8 quadrilaterals. □