A common chord

Let the two intersecting points of the two circles be $P_1(x_1, y_1)$ and $P_2(x_2,y_2)$ . Then $(x_1, y_1)$ and $(x_2,y_2)$ satisfy the two equations.

$\begin{cases} x^2 + y^2 = 16 & ...(1) \\ (x-1)^2 + (y-2)^2 = 25 & ...(2) \end{cases}$ .

From $(2)$ :

$\begin{aligned} \blue{x^2} - 2x + 1 + \blue{y^2} - 4y + 4 & = 25 & \small \blue{\text{Note that }(1): \ x^2 + y^2 = 16} \\ - 2x - 4y & = 4 \\ \implies x + 2y & = - 2 \end{aligned}$ .

The equation $x+2y = -2$ is the straight line passes through $P_1$ and $P_2$ . We need to find the length

$\begin{aligned} P_1P_2 & = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2} \\ & = \sqrt{\blue{x_1^2} - 2x_1x_2 + \red{x_2^2} + \blue{y_1^2} - 2y_1y_2 + \red{y_2^2}} & \small \blue{\text{Note that }(1): \ x^2 + y^2 = 16} \\ & = \sqrt{32 - 2\blue{x_1x_2} - 2\red{y_1y_2}} & \small \blue{\text{By Vieta's formula (see note)}} \\ & = \sqrt{32 + \blue{24} + \red{\frac {24}5}} = \sqrt {\frac {304}5} \approx \boxed{7.797} \end{aligned}$

---

Note: From $x+2y = -2$ , $\implies y = - \dfrac {x+2}2$ . Putting it into $(1)$ , we have:

$\begin{aligned} x^2 + \left(-\frac {x+2}2\right)^2 & = 16 \\ x^2 + \frac {x^2 + 4x+4}4 & = 16 \\ 5x^2 + 4x - 60 & = 0 \\ \implies x^2 + \frac 45x - 12 & = 0 \end{aligned}$

By Vieta's formula , we have $x_1x_2 = -12$ .

Similarly, $x = -2(y+1)$ , $4(y+1)^2 + y^2 = 16 \implies 5y^2 + 8y - 12 = 0$ , $\implies y_1y_2 = - \dfrac {12}5$ .

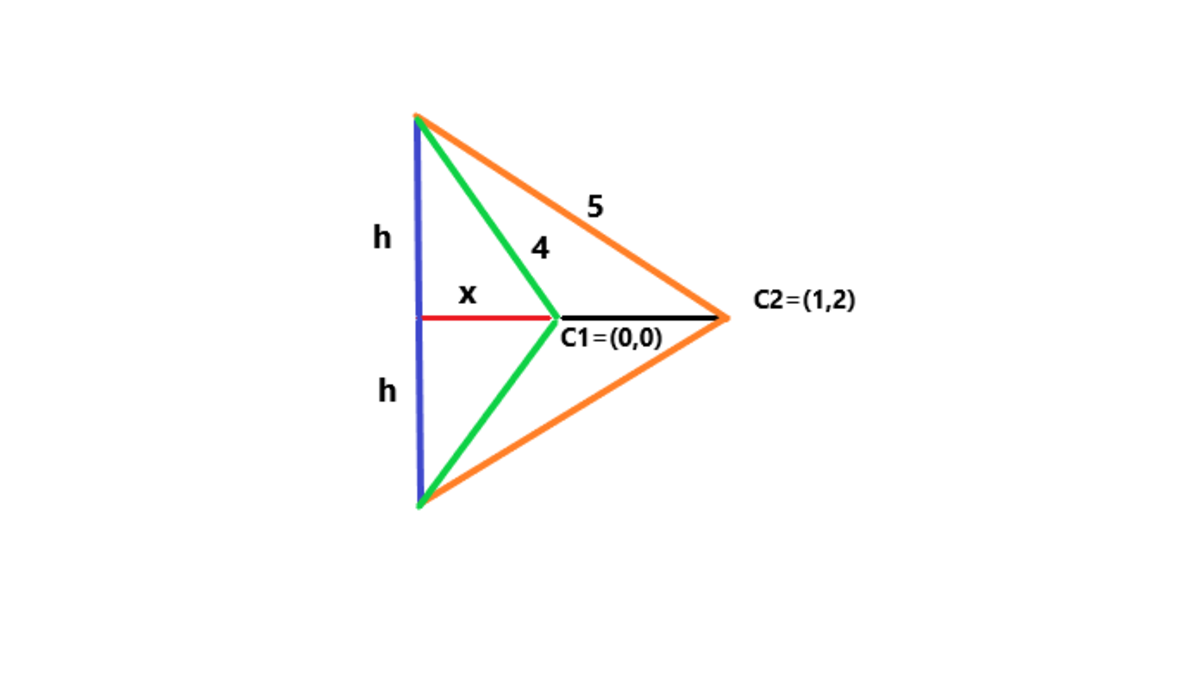
The distance between the centres $= \sqrt{1^2+2^2} = \sqrt{5}$

By Pythagoras theorem,

$4^2 - h^2 = x^2 \\ 5^2 - h^2 = (x+\sqrt{5})^2$

Solving the equations, we have x $= \cfrac{2}{\sqrt{5}}$ and h $= \sqrt{\cfrac{76}{5} }$

The length of the chord $= 2h \approx \boxed{7.797}$

The second circle's center is $\sqrt{1^2 + 2^2} = \sqrt{5}$ away from the origin, so we can change its equation to $(x - \sqrt{5})^2 + y^2 = 25$ (representing a rotation about the origin) and still preserve the distance between intersection points to make the math a little easier.

The circles $x^2 + y^2 = 16$ and $(x - \sqrt{5})^2 + y^2 = 25$ intersect at $(-\frac{2\sqrt{5}}{5}, \pm \frac{2\sqrt{95}}{5})$ , and the distance between these two points is $\frac{4\sqrt{95}}{5} \approx \boxed{7.797}$ .

The first circle is centered at $O_1 (0,0)$ with a radius of $r_1 = 4$ . The second circle is center at $O_2(1, 2)$ with a radius of $r_2 = 5$ .

Let the first intersection point be $A$ , then by drawing the triangle $O_1 O_2 A$ , we find that

$\cos \theta = \dfrac{( r_1 ^ 2 + (1^2 + 2^2) - r_2^2 )}{ 2(4) \sqrt{5}} =- \dfrac{1}{2 \sqrt{5}}$

where $\theta = \angle A O_1 O_2$

It follows that $\sin \theta = \dfrac{\sqrt{19}}{ 2 \sqrt{5} }$

Hence chord length = $2 r_1 \sin \theta = 2 (4) \dfrac{\sqrt{19} }{ 2 \sqrt{5} }= 7.797$

Line $x+2y=-2$ came after substituting first circle to second or $y=\dfrac{-2-x}{2}$ touches either circle at $(\dfrac{-2-\sqrt{304}}{5},\dfrac{-8+\sqrt{304}}{10}), (\dfrac{-2+\sqrt{304}}{5}, \dfrac{-8-\sqrt{304}}{10})$ , again found by substitution of the line to either circle, it's the distance between those two points which can also be approximated at between $(-3.887,0.943)$ and $(3.087, -2.544)$ to $7.7976$ .