A complex integral and its cousin

The change of variable $u = x^4$ gives $\begin{aligned} \int_0^\infty \frac{\ln^2x}{1 + x^4}\,dx & = \; \frac{1}{64}\int_0^\infty \frac{u^{-\frac34}\ln^2 u}{1+u}\,du \; = \; \frac{1}{64}\frac{d^2}{du^2}B(1-u,u) \Big|_{u = \frac14} \\ & = \; \frac{1}{64}\frac{d^2}{du^2}\big(\pi \mathrm{cosec}\,\pi u\big)\Big|_{u = \frac14} \; = \; \frac{1}{64}\pi^3\mathrm{cosec}^2\tfrac14\pi\big(2\cot^2\tfrac14\pi + 1\big) \\ & = \; \frac{3\pi^3\sqrt{2}}{32} \end{aligned}$ making the answer $3 + 3 + 2 + 64 = \boxed{72}$ .

We can obtain the integral with a single logarithm by differentiating the Beta function once instead of twice, obtaining $\int_0^\infty \frac{\ln x}{1 + x^4}\,dx \; = \; \frac{1}{16}\frac{d}{du}\big(\pi \mathrm{cosec}\,\pi u\big)\Big|_{u=\frac14} \; = \; -\frac{\pi^2\sqrt{2}}{16}$

Consider the contour $\mathscr{C} \subset \mathbb{C}$ consisting of the upper-half disk of radius $R > 1$ minus an upper-half disk of radius $r < 1$ , as shown in the following picture.

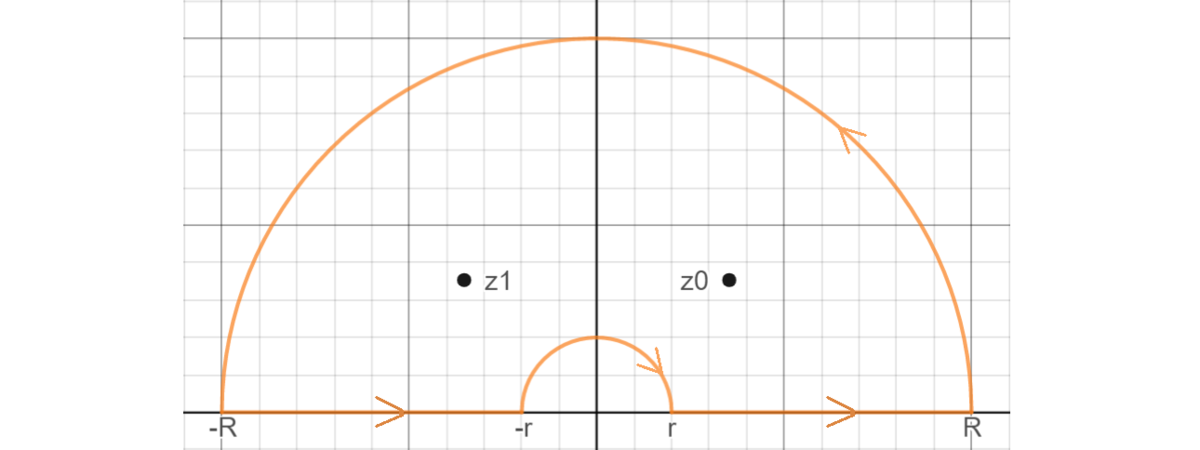(If this can be scaled, please tell me in a comment).

Let $f: \mathbb{C} \to \mathbb{C}$ , $z \mapsto \frac{\log^2(z)}{z^4+1}$ , where $\log: \mathbb{C} \to \mathbb{C}$ , $z \mapsto \log|z| + i\cdot\arg(z)$ , where $-\frac{\pi}{2} < \arg(z) \leq \frac{3\pi}{2}$ denotes the argument of $z$ . We observe that $\oint_\mathscr{C} f(z) \mathrm{d}z = \int_r^R f(x)\mathrm{d}x + \int_{\mathcal{C}_R} f(z)\mathrm{d}z + \int_{-R}^{-r} f(z)\mathrm{d}z + \int_{\mathcal{C}_r} f(z)\mathrm{d}z,$ where $\mathcal{C}_R, \mathcal{C}_r$ denote the parts of the contour over the circles with radius $R, r$ respectively. We will first show that both $\int_{\mathcal{C}_R} f(z)\mathrm{d}z \text{ and } \int_{\mathcal{C}_r} f(z)\mathrm{d}z$ tend to 0 as $R \to \infty$ , $r \to 0$ . First, observe that by the triangle inequality, $|z^4+1| \geq \left||z^4|-|1|\right|$ . Now it follows that $\left|\int_{\mathcal{C}_R} f(z)\mathrm{d}z\right| \leq \pi R \cdot \max_{z\in \mathcal{C}_R} \left|\frac{\log^2(z)}{z^4+1}\right| \leq \pi R \cdot \max_{z\in \mathcal{C}_R} \left|\frac{\log^2(z)}{R^4-1}\right| \leq \pi R \cdot \max_{z\in \mathcal{C}_R} \frac{|\log^2|R||+|i\cdot \arg(z)|}{R^4-1} < \frac{\pi R\log^2(R)+2\pi^2 R}{R^4-1} \xrightarrow{R\to\infty} 0.$ In a similar fashion, it follows that $\left|\int_{\mathcal{C}_r} f(z)\mathrm{d}z\right| \xrightarrow{r\to 0} 0$ by using l'Hôpital's rule at the end.

Now, we will use the Residue Theorem on the contour integral to observe that $\oint_\mathscr{C} f(z)\mathrm{d}z = 2\pi i \cdot \left[\text{Res}_{z=e^{\pi i /4}} f(z) + \text{Res}_{z=e^{3\pi i/4}} f(z) \right].$ By the lemma which will be proven down below, for $a \in \{e^{\pi i k/4}\;|\; k \in \{1,3,5,7\}\}$ : $\text{Res}_{z=a} \frac{\log^2(z)}{z^4+1} = \frac{\log^2(a)}{4a^3}.$ Using this lemma, we obtain $\oint_\mathscr{C} f(z)\mathrm{d}z = 2\pi i \cdot \left[\frac{(\pi i/4)^2}{4e^{3\pi i /4}} + \frac{(3\pi i/4)^2}{4e^{\pi i/4}}\right].$ After doing some algebraic calculations, we see that
$\oint_\mathscr{C} f(z)\mathrm{d}z = -\frac{5\pi^3\sqrt{2}}{32}-i\cdot\frac{\pi^3\sqrt{2}}{8}.$ Letting $R \to \infty, r \to 0$ , we get the equation $\oint_\mathscr{C} f(z) \mathrm{d}z = \int_0^\infty f(x)\mathrm{d}x + \int_{-\infty}^{0} f(z)\mathrm{d}z.$ We will now simplify the latter integral. Note that $\int_{-\infty}^{0} \frac{\log^2(z)}{z^4+1}\mathrm{d}z = \int_{-\infty}^{0} \frac{(\log|z|+\pi i)^2}{z^4+1}\mathrm{d}z = \int_0^\infty \frac{\log^2|x|+2\pi i \log|x| - \pi^2}{x^4+1}\mathrm{d}x.$ By the remark in the problem, $\int_0^\infty \frac{\pi^2}{x^4+1} \mathrm{d}x = \frac{\pi^3\sqrt{2}}{4}.$ Using all information gathered so far, we obtain that $-\frac{5\pi^3\sqrt{2}}{32}-i\cdot\frac{\pi^3\sqrt{2}}{8} = \oint_\mathscr{C} f(z)\mathrm{d}z = 2 \int_0^\infty \frac{\log^2(x)}{x^4+1}\mathrm{d}x + 2\pi i \cdot \int_0^\infty \frac{\log(x)}{x^4+1} \mathrm{d}x - \frac{\pi^3\sqrt{2}}{4}.$ As the integrands are real-valued, we conclude that $\boxed{\int_0^\infty \frac{\log^2(x)}{x^4+1}\mathrm{d}x = \frac{3\pi^3\sqrt{2}}{64} \;\mathrm{ and } \int_0^\infty \frac{\log(x)}{x^4+1}\mathrm{d}x = -\frac{\pi^2\sqrt{2}}{16}.}$ Lemma: For $a \in \{e^{\pi i k/4}\;|\; k \in \{1,3,5,7\}\}$ , $\text{Res}_{z=a} \frac{\log^2(z)}{z^4+1} = \frac{\log^2(a)}{4a^3}.$

Proof. By definition, $\text{Res}_{z=a} \frac{\log^2(z)}{z^4+1} = \lim_{z\to a} \frac{(z-a)\log^2(z)}{z^4+1}$ . By l'Hôpital's rule, $\text{Res}_{z=a} \frac{\log^2(z)}{z^4+1} = \lim_{z\to a} \frac{\log^2(z) + 2(z-a)\log(z)/z}{4z^3} = \frac{\log^2(a)}{4a^3}. \hskip{2em} \blacksquare$