A Complicated Area
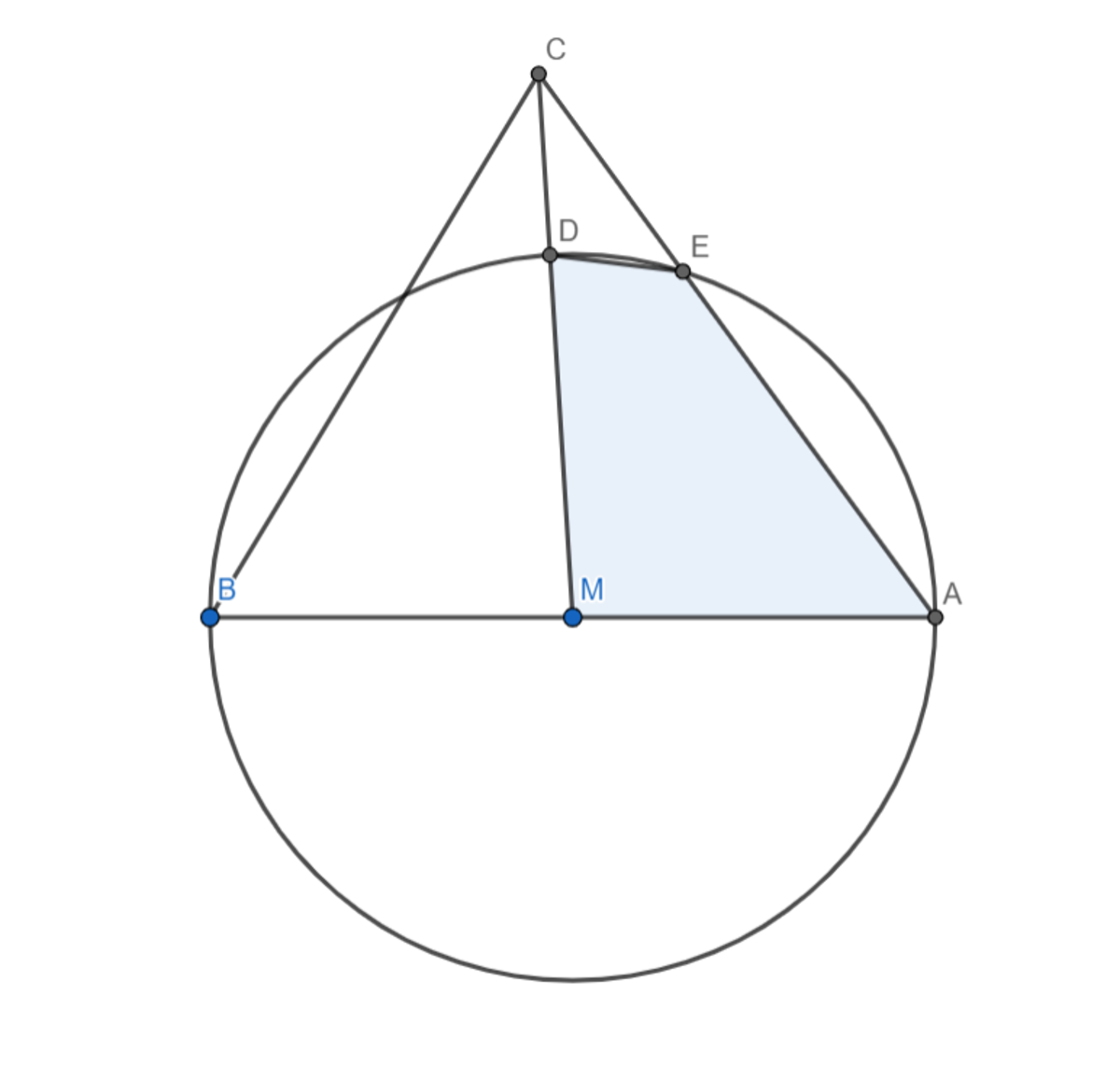
The figure shows that has side lengths , , and with being a diameter of the circle of center . Segments and intersect the circle at points and respectively.
If the area of quadrilateral can be expressed as , where , , and are positive integers, with and being coprime and being square-free, find .
Note: The area does NOT include the space between segment and arc .
The answer is 328.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let us first find the length of C M . From cosine rule ,
{ 5 5 C M 2 = 7 2 + 8 2 − 2 ⋅ 7 ⋅ 8 cos B = 7 2 + 4 2 − 2 ⋅ 7 ⋅ 4 cos B . . . ( 1 ) . . . ( 2 )
For 2 ( 2 ) − ( 1 ) : 2 C M 2 − 5 5 = 7 2 + 2 ( 4 2 ) − 8 2 ⟹ C M = 6 . Then C D = C M − D M = 6 − 4 = 2 . To find C E , we extend C M to meet the circle at F . Then by two secant theorem , we have:
C A ⋅ C E 5 5 ⋅ C E ⟹ C E = C F ⋅ C D = 1 0 ⋅ 2 = 5 5 2 0
We note that the areas of △ B C M and △ A C M are the same and by Heron's formula , for s = 2 7 + 6 + 4 = 8 . 5 , [ B C M ] = 8 . 5 ⋅ 1 . 5 ⋅ 2 . 5 ⋅ 4 . 5 = 4 3 2 5 5 . Also that 2 C A ⋅ C M sin ∠ M C A = 2 5 5 ⋅ 6 sin ∠ M C A = 4 3 2 5 5 , ⟹ sin ∠ M C A = 4 1 1 1 5 1 .
Then the area of quadrilateral A M D E is:
[ A M D E ] = [ A C M ] − [ C D E ] = 2 1 ( C M ⋅ C A − C D ⋅ C E ) sin ∠ M C A = 2 1 ( 6 5 5 − 2 ⋅ 5 5 2 0 ) 4 1 1 1 5 1 = 4 4 2 9 2 5 5
Therefore a + b + c = 2 9 + 2 5 5 + 4 4 = 3 2 8 .