A Complicated Trapezium
Geometry
Level
pending
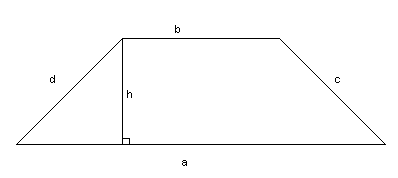ABCD is a trapezium in which AB is parallel to DC , AB = 78 cm , CD= 52 cm , AD = 28 cm , and BC = 30 cm . Find the area of the trapezium .
The answer is 1680.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
In trapezium ABCD where b = AB, c= BC, a = CD and d = AD :
Draw a line BE such BE is parallel to AD
Thus:
AB = 52 BC = 30 CD = 78 CE = 26 BE = AD = 28
Consider triangle BDE:
Using Heron's formula Area of a triangle = (s(s - a)(s -b )(s - c))^(1/2), where a, b, c are the three sides of the triangle s = (a+b+c)/2, we have
s = (28+26+30)/2 = 42
(26 h)/2 = (42 * (42 - 28) (42 - 30)*(42 - 26))^(1/2)
h = (42*8)/13
Thus the area of the trapezium =
[(sum of lengths of the parallel sides) * (h)]/2
= [(78+52) 42 8]/(13*2)
= 1680