A composite function
It is given that f ( x ) = x 3 − 3 x + 1 . Find the number of real roots of f ( f ( x ) ) .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
f ( x ) = x 3 − 3 x + 1 f ′ ( x ) = 3 x 2 − 3 f ′ ( x ) = 0 at x = 1 , − 1 f ( − 1 ) = 3 , f ( 1 ) = − 1 For our final estimation, we see f ( − 2 ) < 0 , f ( 2 ) > 0 .
Thus the 3 roots of
f
(
x
)
=
0
are such that
−
2
<
α
<
−
1
0
<
β
<
1
1
<
γ
<
2
Now estimate the graph of
f
(
x
)
.
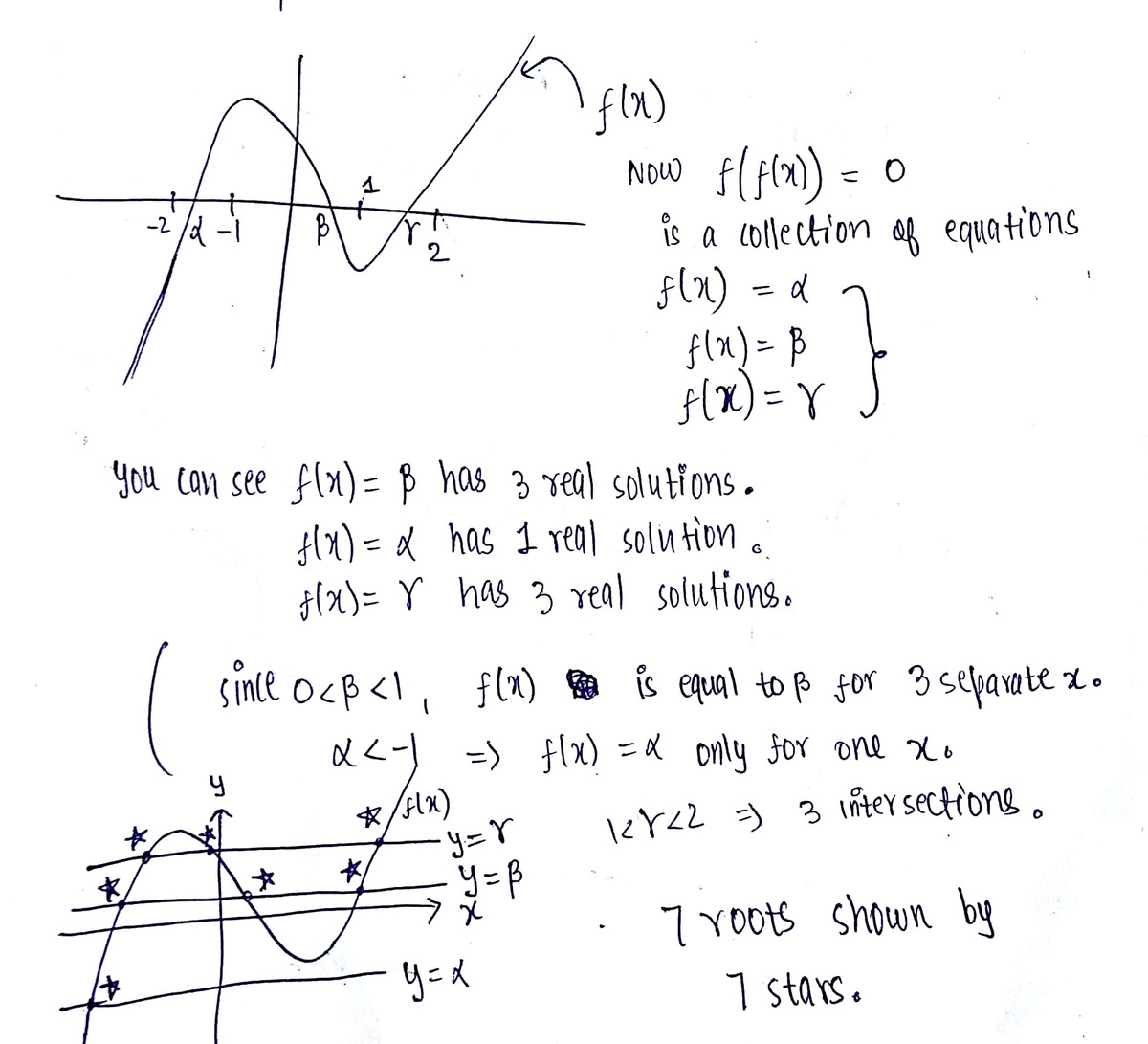
We could easily solve the problem without any rigorous calculation or actually solving the 9 degree resulting polynomial. Cheers!
suppose f(x) has A , B ,C as its roots, then f(f(x))=0 when f(x) = A,B or C. So , draw the graph of f(x) and then draw lines of Y=A, Y=B , Y=C. These will intersect at 7 points!!!