A composite of a cone and a sphere
A right circular cone has it apex at and it circular base is centered at the origin and has a radius of . Intersecting with the cone is a sphere centered at with a radius of . Find the volume of the portion of the sphere that lies outside the cone, and report the value of .
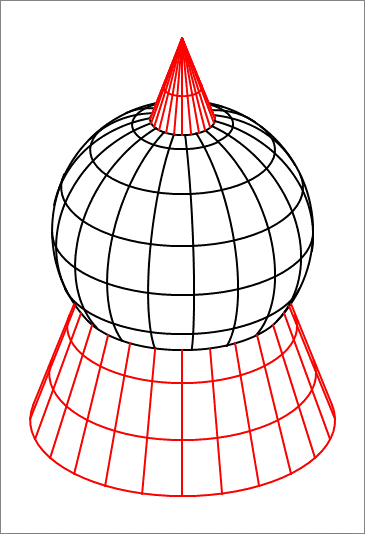
The answer is 490366.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
In the cross-section, say in the x z plane, the composite appears as a triangle superimposed on a circle, as shown below.
Let θ 0 be the semi-vertical angle of the cone, then
θ 0 = tan − 1 2 2 1
The equation of its slant edge is z = 2 0 − ( cot θ 0 ) x
while the parametric equation of the circle is ( x , z ) = ( 6 sin θ , 0 , 1 0 + 6 cos θ )
Plugging in the second equation into the first, we can find the angles θ where the surface of the sphere intersects the surface of the cone. And this turns out to be at θ 1 = 0 . 2 4 9 1 9 4 and at θ 2 = 2 . 2 1 2 7 2 .
Now, the area of the surface of the sphere that is outside the cone is given by
A s = 2 π R 2 ( cos θ 1 − cos θ 2 )
where R = 6 is the radius of the sphere. The area of the cone that lies inside the sphere is given by
A c = π ( r 2 s 2 − r 1 s 1 ) = π R 2 ( sin 2 θ 2 − sin 2 θ 1 ) ( sin θ 0 1 )
Taking as our pivot point the center of the sphere, the required volume can be written as
V = 3 1 ( R A s − d A c )
where d is the (constant) perpendicular distance from the center of the sphere to the surface of the cone. It is given by
d = 1 0 sin θ 0
Evaluating the above, we obtain V = 4 9 0 . 3 6 6 3 . . . ; therefore the answer is ⌊ 1 0 0 0 V ⌋ = 4 9 0 3 6 6 .