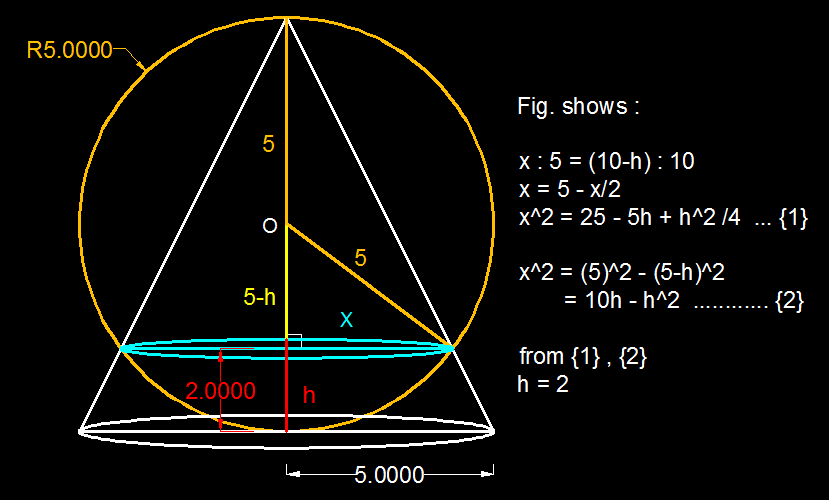
A Cone and a Sphere!

Geometry Level 4

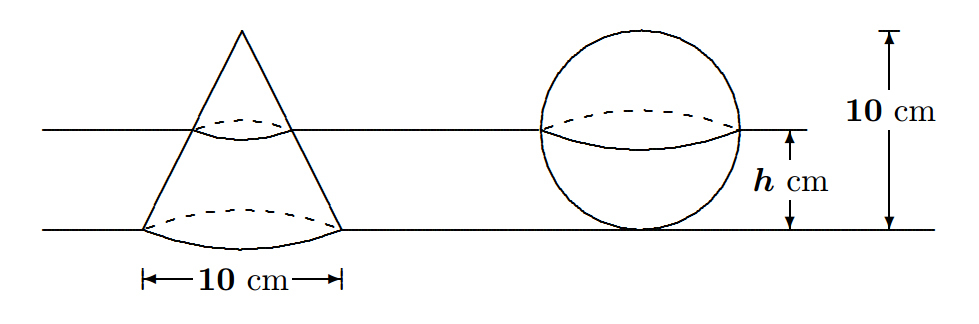
In the diagram above, the sphere has a diameter of 10 cm 10 \text{ cm} . Also, the right circular cone has a height of 10 cm, and it's base has a diameter of 10 cm 10 \text{ cm} . The sphere and the cone stand on a horizontal surface. If a horizontal plane cuts both the sphere and the cone, the cross-sections will both be circles as shown.

Find the height of the horizontal plane (from the bottom) (in cm \text{cm} ) that gives circular cross-sections of the sphere and cone of equal area. Note that the height should be less than 10 cm 10 \text{ cm} .

Bonus : A sphere of diameter d d and a right circular cone with a base of diameter d d stand on a horizontal surface. In this case, the height of the cone is equal to the radius of the sphere. Show that, for any horizontal plane that cuts both the cone and the sphere, the sum of the areas of the circular cross-sections is always the same.

1 5 8 2 3 7 6 4

Satyajit Mohanty by Satyajit Mohanty , 24, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Ahmad Saad
May 12, 2016

4 Helpful 0 Interesting 0 Brilliant 0 Confused

The solution by Ahmad Saad is beautiful. Below is another approach. Probably a common approach.
Let Y be the distance of the section from the top. Same for both Cone and sphere. Let X_{c\ or\ s} be the radius at Y. F o r t h e c o n e Y X c = d 1 2 ∗ d . S o X c = 1 2 ∗ Y , ∴ X c 2 = 1 4 ∗ Y 2 . F o r t h e s p h e r e X s 2 = ( 1 2 ∗ d ) 2 − ( 1 2 ∗ d − Y ) 2 = d Y − Y 2 . F o r s a m e a r e a w e m u s t h a v e X c 2 = X s 2 . ⟹ 1 4 ∗ Y 2 = 10 Y − Y 2 , ∴ Y = 8. S o h e i g h t f r o m t h e b o t t o m = 10 − 8 = 2. For\ the\ cone\ \dfrac Y X_c=\dfrac d {\frac 1 2 *d}.\ \ So\ X_c=\frac 1 2*Y, \ \ \therefore \color{#3D99F6}{X_c^2=\frac 1 4 *Y^2} .\\ For\ the\ sphere\ \color{#3D99F6}{ X_s^2=(\frac 1 2 *d)^2 - (\frac 1 2 *d - Y)^2=dY - Y^2}.\\ For\ same\ area\ we\ must\ have\ X_c^2=X_s^2.\\ \implies\ \ \frac 1 4 *Y^2=10Y - Y^2,\ \ \therefore\ Y=8.\\ So\ \ height\ from \ the\ bottom\ =10-8=2.\\\ \ \ \\

Bonus:
Let Y be the distance of the sections from the top . Let X c and X s be the radius of Cone and Sphere respectively at Y. F o r t h e c o n e Y X c = 1 2 ∗ d 1 2 ∗ d S o X c = Y , ∴ X c 2 = Y 2 . F o r t h e s p h e r e X c 2 = ( 1 2 ∗ d ) 2 − Y 2 . S u m o f a r e a a t A N Y s e c t i o n Y , = π ∗ ( Y 2 + ( 1 2 ∗ d ) 2 − Y 2 ) = ( π 2 ∗ d ) 2 = c o n s t a n t . For\ the\ cone\ \dfrac Y {X_c}=\dfrac {\frac 1 2 *d} {\frac 1 2 *d}\ \ So\ X_c=Y, \ \ \therefore \color{#3D99F6}{X_c^2=Y^2} .\\ For\ the\ sphere\ \color{#3D99F6}{ X_c^2=(\frac 1 2 *d)^2-Y^2}.\\ Sum \ of\ area\ at\ ANY \ section\ Y, =\pi*( Y^2 + (\frac 1 2 *d)^2-Y^2)=(\frac \pi 2 *d)^2=constant.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

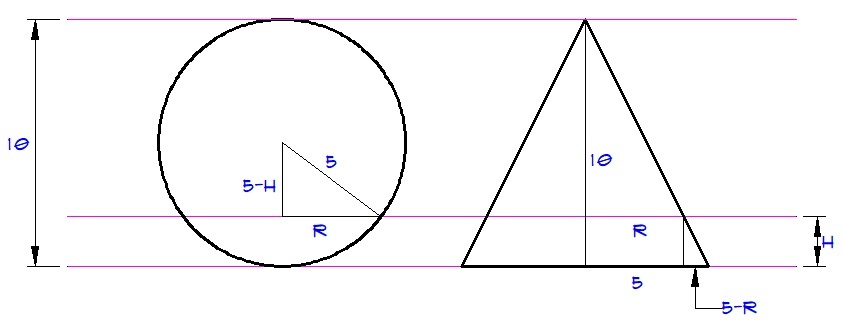Considering the sphere. We have

5 2 = ( 5 − h ) 2 + r 2 5^2=(5-h)^2+r^2

r 2 = − h 2 + 10 h r^2=-h^2+10h ⟹ \implies 1 \color{#D61F06}\boxed{1}

Considering the cone. We have

5 − r h = 5 10 \dfrac{5-r}{h}=\dfrac{5}{10}

r = 5 − 1 2 h r=5-\dfrac{1}{2}h

Squaring both sides we get,

r 2 = 25 − 5 h + h 2 4 r^2=25-5h+\dfrac{h^2}{4} ⟹ \implies 2 \color{#D61F06}\boxed{2}

1 \color{#D61F06}\boxed{1} = = 2 \color{#D61F06}\boxed{2}

− h 2 + 10 h = 25 − 5 h + h 2 4 -h^2+10h=25-5h+\dfrac{h^2}{4}

h 2 − 12 h + 20 = 0 h^2-12h+20=0

h = 2 h=2 or h = 10 h=10

The desired answer is h = 2 \boxed{h=2}

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...