A constrained pulley!

Classical Mechanics Level 2

The system is initially kept at rest, but is now released.
Find the $\green{\underline{\text{acceleration}}}$ of the $\green{\underline{5 \text{kg}}}$ block in $\red{\underline{\text{ms}^{-2}}}$ . Let it be $\green{a}$ .
Find the $\orange{\underline{\text{tension}}}$ of the $\orange{\underline{\text{Rope 2}}}$ block in $\red{\underline{\text{newtons}}}$ . Let it be $\orange{T}$ .
Enter your answer as the $\green{|a|}+\orange{|T|}$ , rounded up to two decimal places.

$\underline{\red{\text{Details and assumptions.}}}$

All strings and pulleys are ideal.
Ignore air resistance.
Assume the ceiling is rigid.
Take $\purple{\underline{\text{Acceleration due to gravity = 10 ms}^{-2}}}$

$\boxed{\large{\text{Difficulty: }\color{#D61F06}{\text{Small, but pointy}}} \LARGE{\red{\dagger \dagger } \dagger \dagger \dagger}}$

This problem is original.

The answer is 36.67.

2 solutions

Vinayak Srivastava
Sep 2, 2020

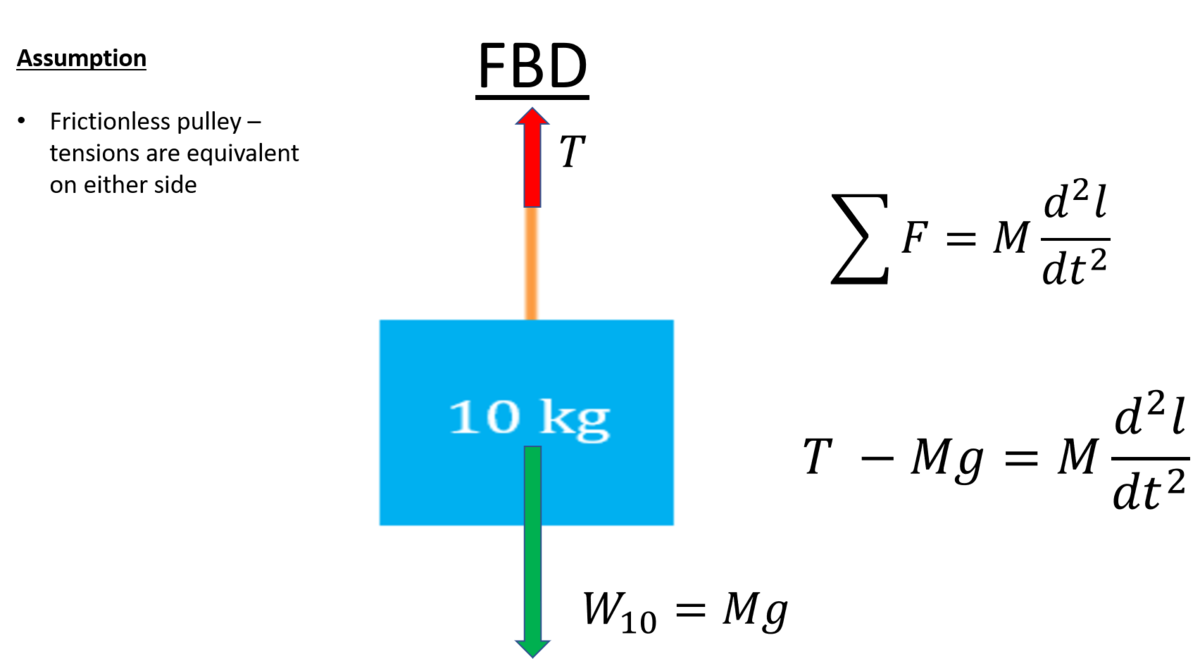
The tension in Rope 2 is $T$ . So tension in Rope 3 is $T+T=2T$ .

By Tension Constraint,

$\begin{aligned} {\displaystyle \sum} {T \cdot a} &= 0 \\ T \cdot {a_{10 \text{kg}}} &= 2T \cdot a \\ \implies {a_{10 \text{kg}}} &=2a \\ \end{aligned}$

From FBD of both the blocks,

$\begin{aligned} 2T-5g &=5a &(1)\\ 10g - T &= 10 {a_{\text{10 kg}}} \\ \implies 20g -2T &= 40a & (2)\\ \text{Adding the equations } (1) \text{ and } (2) &~\\ 15g &= 45a \\ \implies a&=\dfrac{g}{3} \\ \text{Putting value of } a \text{ in any of the equations, we can get: } &~ \\ T &= \dfrac{10g}{3} \\ \implies |T|+|a| &= \dfrac{11g}{3} \approx \boxed{36.67} \\ \end{aligned}$

@Vinayak Srivastava Upvotes have been awarded.
I wonder Again a very difficult problem. Now, I will consider this problem as the most hardest problem ever i have seen.

Talulah Riley - 9 months, 1 week ago