A Constrained Triangle
What is the maximum area of a triangle with inradius = 1 and circumradius = 3?
The answer is 7.10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Since the base of the triangle changes as well as its height, it is not automatic that the first line you draw has to be the base of an isosceles triangle.
You argument does not cover all the options adequately.
If you look at my solution, the pink triangle is quite close to being a maximum area triangle, and there is a maximum area triangle where the base (the vertical line) is one of the two equal sides of an isosceles triangle.
Let us consider triangles A B C with inradius r and circumradius R > 2 r (we exclude equilateral triangles by avoiding R = 2 r ). Then standard results tell us that R = cos A + cos B + cos C − 1 r = 4 sin 2 1 A sin 2 1 B sin 2 1 C r while the area of the triangle is Δ = 2 R 2 sin A sin B sin C = 4 R r cos 2 1 A cos 2 1 B cos 2 1 C Putting u = 2 1 A , v = 2 1 B , w = 2 1 C , we need to maximize the quantity Δ = 4 R r cos u cos v cos w subject to the constraints u , v , w > 0 u + v + w = 2 1 π sin u sin v sin w = 4 R r The method of Lagrange multipliers leads us to solve the equations − 4 R r sin u cos v cos w − λ cos u sin v sin w − μ − 4 R r cos u sin v cos w − λ sin u cos v sin w − μ − 4 R r sin u sin v cos w − λ sin u sin v cos w − μ = 0 = 0 = 0 for some λ , μ . Eliminating μ leads to the equations sin ( u − v ) [ λ sin w − 4 R r cos w ] = sin ( v − w ) [ λ sin u − 4 R r cos u ] = sin ( w − u ) [ λ sin v − 4 R r cos v ] = 0 If sin ( u − v ) , sin ( v − w ) , sin ( w − u ) are all nonzero, we deduce that tan u = tan v = tan w = 4 R r λ and hence, since u , v , w are all acute, u = v = w = 6 1 π , which would imply that R = 2 r . Since we have excluded this case, we deduce that one of the sines must be zero. Without loss of generality, we shall assume that u = v , and so sin 2 u sin ( 2 1 π − 2 u ) = sin u sin v sin w ( 1 − cos 2 u ) ( 2 cos 2 u − 1 ) = sin 2 u cos 2 u 2 cos 4 u − 3 cos 2 u + 1 + 4 R r 2 ( cos 2 u − 4 3 ) 2 = 4 R r = 4 R r = 0 = 8 R R − 2 r = 8 R 2 d 2 where d = R 2 − 2 R r is the distance between the incentre and circumcentre of A B C . Thus Δ is extremized when u = u ± , where cos 2 u ± = 4 R 3 R ± d sin 2 u ± = 4 R R ∓ d Thus the extremal areas of a triangle with inradius r and circumradius R are Δ ± = 4 R r cos 2 u ± cos ( 2 1 π − 2 u ± ) = 4 R r cos 2 u ± sin 2 u ± = 8 R r cos 3 u ± sin u ± = 8 R r ( 4 R 3 R ± d ) 2 3 ( 4 R R ∓ d ) 2 1 = 2 R r ( 3 R ± d ) ( 3 R ± d ) ( R ∓ d ) = 2 R r ( 3 R ± d ) 3 R 2 − d 2 ∓ 2 R d = r ( 3 R ± d ) 2 R R + r ∓ d Since Δ − 2 − Δ + 2 = 4 r 2 d ( R − 2 r ) ≥ 0 we deduce that the maximum triangle area is Δ − = r ( 3 R − d ) 2 R R + r + d With R = 3 , r = 1 , we obtain d = 3 and Δ − = 2 1 ( 3 3 − 1 ) 4 + 3 ≈ 7 . 1 0 3 8 0 8 9 5 1
The blue and brown isosceles triangles, with parallel bases, are the extreme-area triangles. The blue triangle yields the maximum area, while the brown triangle yields the minimum area. A triangle with inradius 1 and circumradius 3 (although not necessarily isosceles) can be found with one side parallel to the two bases of the extreme-area triangles and lying between them - the pink triangle is an example.
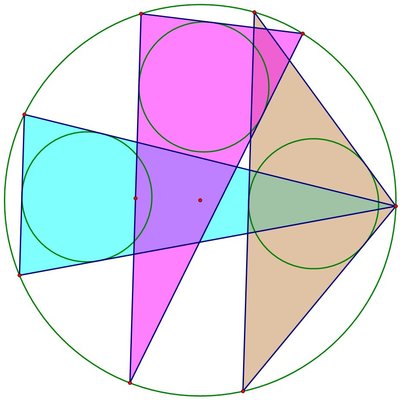
You were right, @Mark Hennings , the reasoning behind my proof was incorrect, so I deleted it. Thanks for pointing it out!
Choose any line segment as a base for the triangle, the outer circle should pass through its endpoints. Maximal triangle surface is obtained with the top point at maximal height. Therefore the top should be above the centerpoint of the line segment.
Choose the x-axis as the baseline of the triangle. (p, 0) and (-p, 0) as the two base points. The inner circle has radius 1, determine the top of the triangle (0, 2p^2/(p^2-1)). The centerpoint of the outer circle is (0, 2p^2/(p^2-1)-R).
The distance between the centerpoint of the outer circle and (p, 0) should be R=3, the radius of the outer circle. This yields to p^6-10p^4+13p^2=0. Surface of the triangle is A=p.2p^2/(p^2-1). Two solutions for p apart from 0 or nagative solutions. Largest surface for p^2=5-2sqrt(3). A=7.1038...