A cool geometry problem!
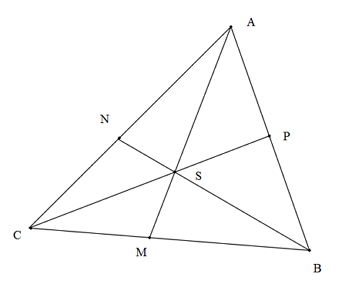In the given figure,
S
is the circumcentre of
△
A
B
C
.Then find the value of
A
M
R
+
B
N
R
+
C
P
R
,where
R
is the circumradius of the
△
A
B
C
.
The answer is 2.0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Moderator note:
Standard explanation of this geometric identity.
sorrcy could u explain the part similarly
Log in to reply
Sure,sorry. B N B S = a r ( A B S ) / a r ( A B N ) = a r ( B S C ) / a r ( B N C ) = [ a r ( a b c ) − a r ( A S C ) ] / a r ( A B C )
I'm confused. How do you get from [ A B M ] [ A B S ] to [ M S C ] [ A S C ] ?
I believe every occurrence of [MSC] should be [AMC], otherwise the chain equality fails at the second equal sign - you have a ratio < 1 on the left of it and a ratio on the right of it > 1 .
R means AS or BS or CS,AS:AM is2:3 Then 2/3 plus 2/3 plus 2/3 is 6/3 is 2
This is not valid except for an equilateral triangle. Consider C(0,0), B(6,0) and A(3,4). Careful analysis will show AS:AM is 25:32 and both BS:BN and CS:CP are 39:64. For the general case, the 3 ratios are all different but add up to 2 ! I believe Adarsh Kumar has a general solution if the [MSC] is replaced by [AMC].
The ⅔ ratio is for Centroid and not circumcenters.
Log in to reply
True, but since we are told that in the diagram that the perpendicular bisectors pass through the three angles, it must therefore be an equilateral triangle.
Since there are no numbers present here,we get motivated to use sides as R and hence the required expression becomes, A M R + B N R + C P R = A M A S + B N B S + C P C S .Now,we write the ratio of sides as a ratio of areas of two triangles, A M A S = [ A B M ] [ A B S ] = [ M S C ] [ A S C ] = [ A B M ] + [ M S C ] [ A B S ] + [ A S C ] = [ A B C ] [ A B C ] − [ B S C ] = 1 − [ A B C ] [ B S C ] . Similarly writing the ratios for other sides as well and adding,we get, 1 + 1 + 1 − [ A B C ] [ B S C ] + [ A S C ] + [ A B S ] = 3 − 1 = 2 .In the above solution [ . . ] stands for the area of the specific shape.And done!