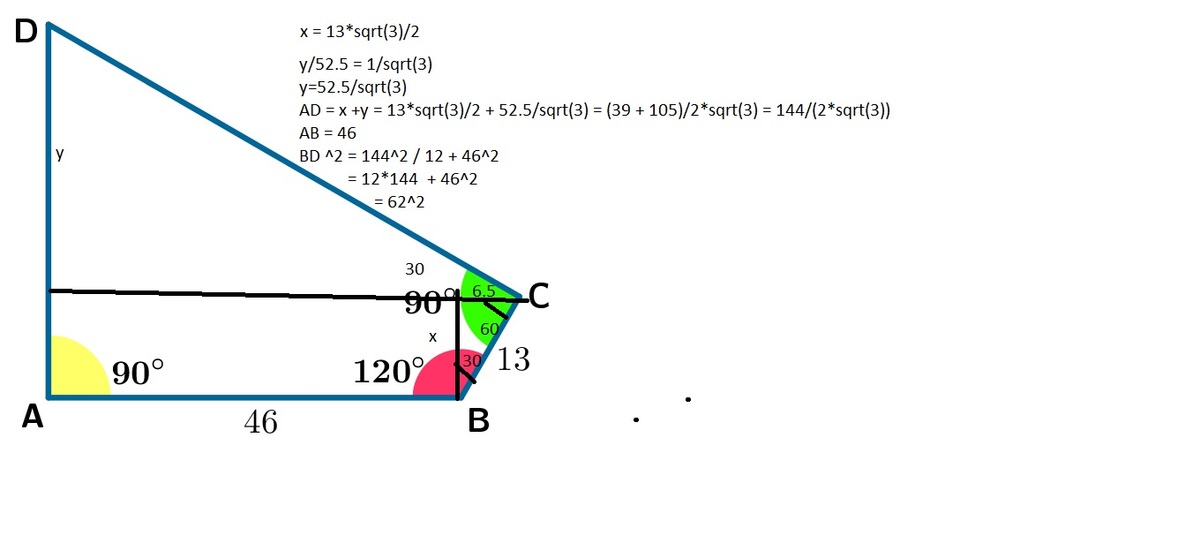
A correct problem, I believe
The
A
B
C
D
is a quadrilateral, such that
∠
D
A
B
=
∠
B
C
D
=
9
0
°
,
∠
A
B
C
=
1
2
0
°
. We know that
A
B
=
4
6
and
B
C
=
1
3
.
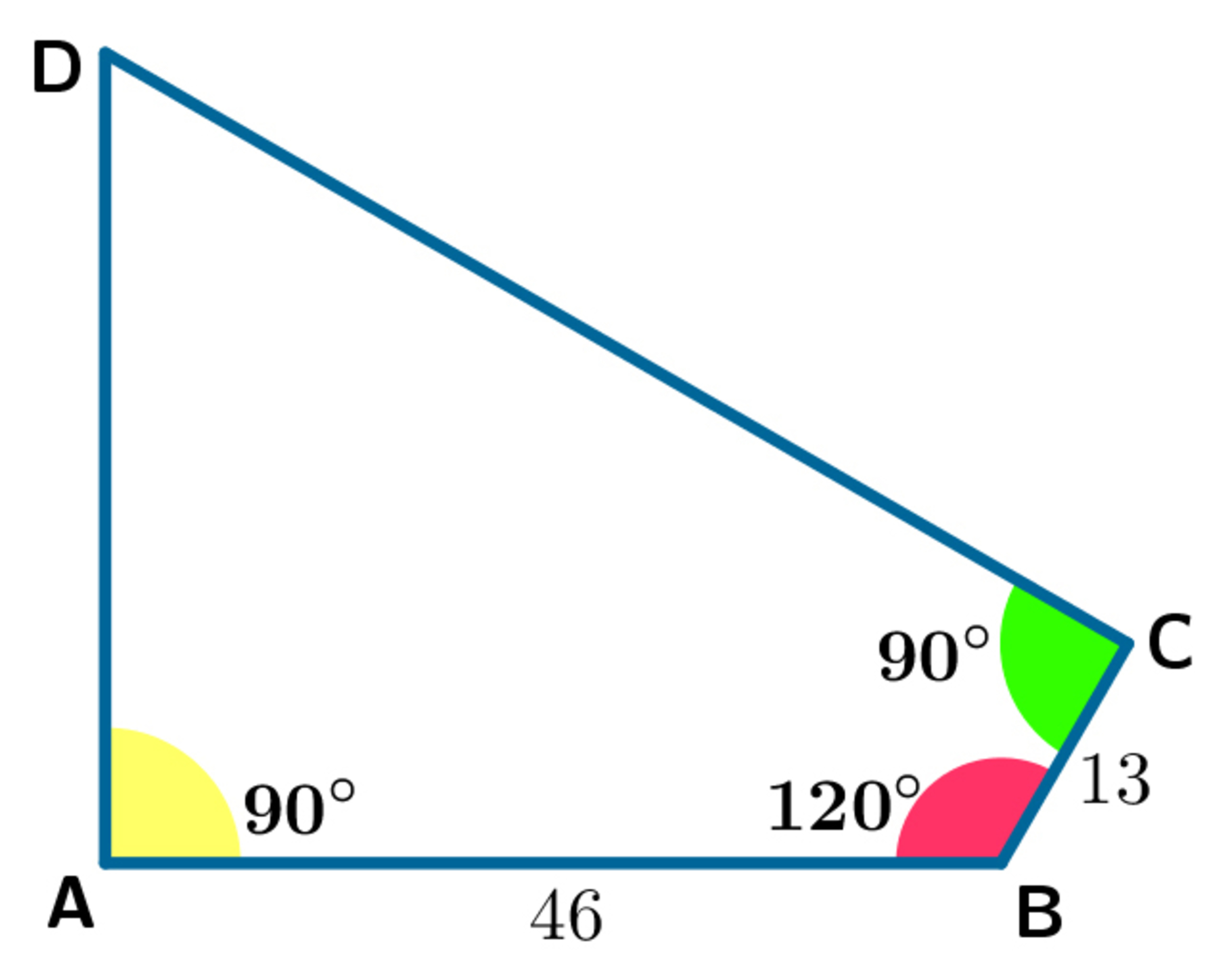
How long is the diagonal B D ?
The answer is 62.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
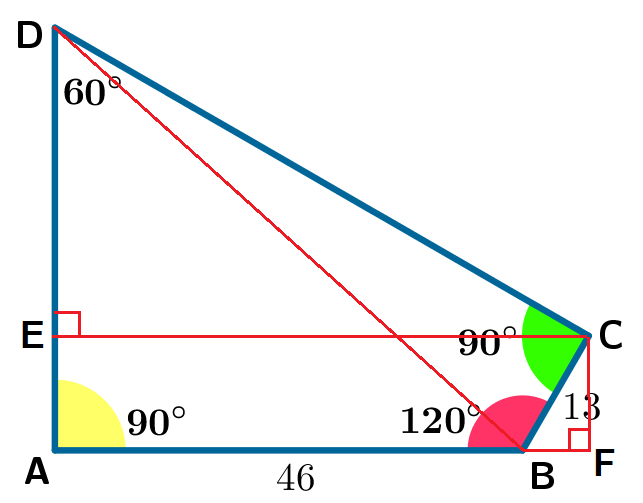
Let C E be parallel to A B , then C E is perpendicular to A D . Drop a perpendicular C F from C to the extension of A B .
Then, we note that C E = A B + B C cos ∠ C B F = 4 6 + 1 3 cos 6 0 ∘ = 5 2 . 5 . Since the sum of internal angles of a quadrilateral is 1 8 0 ∘ , we note that ∠ A D C = 6 0 ∘ . Then tan ∠ A D C = D E C E ⟹ D E = tan 6 0 ∘ C E = 3 5 2 . 5 = 2 3 5 3 .
By Pythagorean theorem , we have
B D 2 ⟹ B D = A B 2 + D A 2 = A B 2 + ( D E + E A ) 2 = A B 2 + ( D E + C F ) 2 = A B 2 + ( D E + B C sin 6 0 ∘ ) 2 = 4 6 2 + ( 2 3 5 3 + 2 1 3 3 ) 2 = 2 1 1 6 + 1 7 2 8 = 3 8 4 4 = 3 8 4 4 = 6 2
Law of cosines in △ A B C provides A C = 4 6 2 + 1 3 2 − 2 × 4 6 × 1 3 × cos 1 2 0 ∘ = 3 1 3
The quadrilateral is cyclic with B C a diameter of the circumcircle of A B C
The formula for radius of circumcircle is r = 4 A a b c , where a , b , c are sides of the triangle and A is its area.
A = 2 1 A B × B C × sin 1 2 0 ∘
r = 4 × 2 1 × 4 6 × 1 3 × 2 3 4 6 × 1 3 × 3 1 3 = 3 1
D B = 2 r = 6 2