A cruel and fickle king
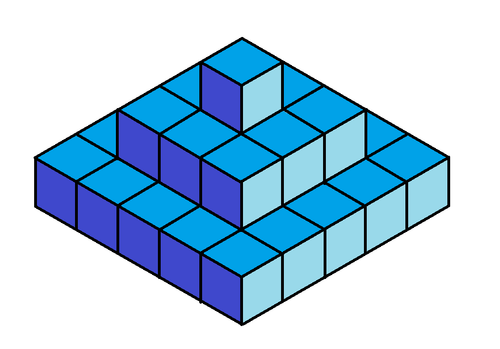 For the past decade, the king of
Mathlandia
has forced his subjects to build a pyramid in his honor. The king decreed the pyramid to be constructed with cubic stone slabs. The king also decreed the pyramid to be built in 100 square levels, with each subsequent level 2 units less on a side than the previous level. The top level was to be constructed with a single cube. (See the picture for an example of a pyramid 3 levels high constructed in the same way).
For the past decade, the king of
Mathlandia
has forced his subjects to build a pyramid in his honor. The king decreed the pyramid to be constructed with cubic stone slabs. The king also decreed the pyramid to be built in 100 square levels, with each subsequent level 2 units less on a side than the previous level. The top level was to be constructed with a single cube. (See the picture for an example of a pyramid 3 levels high constructed in the same way).
Moments after the final cube was placed, the king changed his mind. He ordered the pyramid to be taken down, and in its place, a cubic monolith was to be built. He ordered the monolith to be built as large as possible with the same stone slabs the pyramid was made of.
The king would tolerate no waste, so he ordered one of his subjects to be sacrificed for each leftover slab of stone.
How many of the king's subjects will be sacrificed?
The answer is 2300.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Working this problem, I wrote the first few partial sums of the series 1 2 + 3 2 + 5 2 + 7 2 + ⋯ : 1 , 1 0 , 3 5 , 8 4 , 1 6 5 , … This "feels" very much like Pascal's triangle... indeed, it appears that n terms 1 2 + 3 2 + 5 2 + ⋯ + ( 2 n − 1 ) 2 = ( 2 n + 1 3 ) . (Proof: see below.)
The number of stones is therefore ( 2 0 1 3 ) = 3 ⋅ 2 ⋅ 1 2 0 1 ⋅ 2 0 0 ⋅ 1 9 9 = 6 7 ⋅ 1 0 0 ⋅ 1 9 9 = 1 3 3 3 3 0 0 , which is easily recognized as slightly more than 1 3 3 1 0 0 0 = 1 1 0 3 . The answer is therefore 1 3 3 3 3 0 0 − 1 3 3 1 0 0 0 = 2 3 0 0 .
Proof of the claim made above, by induction:
-
Clearly, for just one term we have 1 2 = 1 = ( 3 3 ) .
-
Suppose the statement is true for n . We will prove it is also true for n ′ = n + 1 . Add the ( n + 1 ) th term: ( 1 2 + 3 2 + 5 2 + ⋯ + ( 2 n − 1 ) 2 ) + ( 2 n + 1 ) 2 = ( 2 n + 1 3 ) + ( 2 n + 1 ) 2 = 6 ( 2 n + 1 ) ( 2 n ) ( 2 n − 1 ) + ( 2 n + 1 ) 2 = 6 2 n + 1 ( ( 2 n ) ( 2 n − 1 ) + 6 ( 2 n + 1 ) ) = 6 2 n + 1 ( 4 n 2 + 1 0 n + 6 ) = 6 2 n + 1 ( 2 n + 2 ) ( 2 n + 3 ) = 6 ( 2 n ′ + 1 ) ( 2 n ′ ) ( 2 n ′ − 1 ) = ( 2 n ′ + 1 3 ) .
Another way to find the sum of the odd squares is to simply add the sum of all of the squares up to 199, and then subtract the even squares up to 198, which can be recognized as 4 times the sum of all of the squares up to 99.
The number of cubic stones in the pyramid will be the sum of the first 100 squares of odd numbers. We can write and simplify the finite series:
k = 1 ∑ 1 0 0 ( 2 k − 1 ) 2 = k = 1 ∑ 1 0 0 ( 4 k 2 − 4 k + 1 ) = 4 k = 1 ∑ 1 0 0 k 2 − 4 k = 1 ∑ 1 0 0 k + 1 0 0
These series can be calculated using the sum of squares formula and the sum of natural numbers formula:
k = 1 ∑ n k 2 = 6 n ( n + 1 ) ( 2 n + 1 )
k = 1 ∑ n k = 2 n ( n + 1 )
Using these formulas, we obtain the number of stones in the pyramid to be 1 3 3 3 3 0 0 . The largest perfect cube less than this number is 1 1 0 3 = 1 3 3 1 0 0 0 . Thus, there are 2 3 0 0 stones left over.