A cube, an octahedron, and a volume
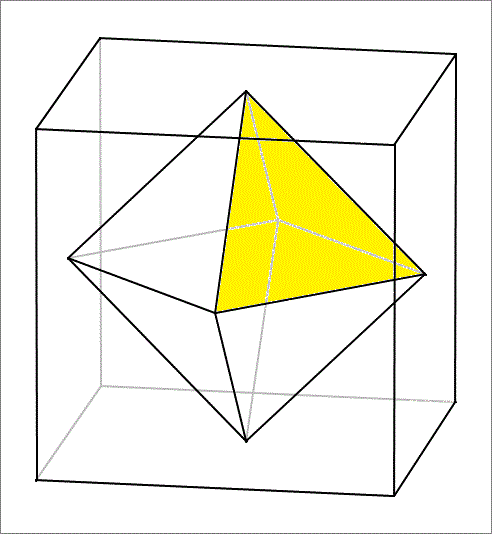
Given a cube of side length , you construct the regular octahedron whose vertices are the centers of the faces of the cube, as shown in the above figure. Pick one of the upper faces of the octahedron (shaded in yellow). You extend the plane of the face in all directions. What is the volume of the portion of the cube that lies above this plane.
The answer is 36.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the vertices of the cube have coordinates of ( ± 3 , ± 3 , ± 3 ) , so that the vertices of the yellow triangle are ( 3 , 0 , 0 ) , ( 0 , 3 , 0 ) , and ( 0 , 0 , 3 ) .
Then the equation of the plane containing the yellow triangle is x + y + z = 3 , which passes through three of the cube's vertices ( 3 , 3 , − 3 ) , ( 3 , − 3 , 3 ) , and ( − 3 , 3 , 3 ) .
Therefore, the volume of the portion of the cube that lies above this plane is a right-angled tetrahedron, which has a volume of 6 1 6 3 = 3 6 .